Goodness of fit

1. Introduction

The ospsuite.plots library provides functions to compare predicted and observed data and resulting residuals:

plotPredVsObs() (see section 2): plot predicted values versus corresponding observed values.
plotResVsCov() (see section 3): plot residuals as points versus a covariate (e.g., Time, observed values, or Age).
plotRatioVsCov() (see section 4): plot ratios as points versus a covariate (e.g., Time, observed values, or Age).
plotQQ() (see section 5): Quantile-Quantile plot.

In these functions, the aesthetics observed and predicted can be used. These aesthetics are also available in other functions of the ospsuite.plots library:

plotBoxwhisker() (see section 6.1): aggregate residuals and display aggregated values versus covariate.
plotHistogram() (see section 6.2): generates histograms of residuals.

The functions plotPredVsObs(), plotResVsCov(), and plotRatioVsCov() are mainly wrappers around the function plotXVsY(), using different defaults for input variables. So, use ?plotXvsY to get more details.

For DDI comparison, the functions plotPredVsObs() and plotResVsObs() can be overlaid with lines indicating the limits of the Guest Criteria (https://dmd.aspetjournals.org/content/39/2/170) (see section 7).

1.1 Setup

This vignette uses the ospsuite.plots and tidyr libraries. We will use the default settings of ospsuite.plots (see vignette(“ospsuite.plots”, package = “ospsuite.plots”)).

library(ospsuite.plots)
library(tidyr)

oldDefaults <- setDefaults()

1.2 Example Data

This vignette uses two randomly generated example datasets provided by the package.

1.2.1 Dataset with Predicted and Observed Data

data <- exampleDataCovariates %>%
  dplyr::filter(SetID == "DataSet2") %>%
  dplyr::select(c("ID", "Age", "Obs", "gsd", "Pred", "Sex"))

knitr::kable(head(data), digits = 3, caption = "First rows of example data.")

First rows of example data.
ID	Age	Obs	gsd	Pred	Sex
1	44	28.808	1.009	32.535	Female
2	23	77.476	0.992	76.418	Male
3	26	35.861	1.028	34.282	Female
4	20	62.711	1.072	55.015	Male
5	21	30.475	1.045	29.751	Female
6	48	74.238	0.989	67.357	Male


metaData <- attr(exampleDataCovariates, "metaData")
metaData <- metaData[intersect(names(data), names(metaData))]
knitr::kable(metaData2DataFrame(metaData), digits = 2, caption = "List of meta data")

List of meta data
	Age	Obs	Pred
dimension	Age	Clearance	Clearance
unit	yrs	dL/h/kg	dL/h/kg

1.2.2 Dataset for Examples with DDI Prediction

dDIdata <- exampleDataCovariates %>%
  dplyr::filter(SetID == "DataSet3") %>%
  dplyr::select(c("ID", "Obs", "Pred")) %>%
  dplyr::mutate(Study = paste("Study", ID))

dDIdata$Study <- factor(dDIdata$Study, levels = unique(dDIdata$Study))

knitr::kable(head(dDIdata), digits = 2, caption = "First rows of dataset used for DDI example.")

First rows of dataset used for DDI example.
ID	Obs	Pred	Study
1	0.53	0.83	Study 1
2	1.20	0.90	Study 2
3	0.43	0.50	Study 3
4	4.93	3.39	Study 4
5	1.39	1.10	Study 5
6	0.44	0.39	Study 6


dDImetaData <- list(
  Obs = list(dimension = "DDI AUC Ratio", unit = ""),
  Pred = list(dimension = "DDI AUC Ratio", unit = "")
)

knitr::kable(metaData2DataFrame(dDImetaData), digits = 2, caption = "List of meta data")

List of meta data
	Obs	Pred
dimension	DDI AUC Ratio	DDI AUC Ratio
unit

1.2.3 Dataset for Ratio Comparison

pkRatioData <- exampleDataCovariates %>%
  dplyr::filter(SetID == "DataSet1") %>%
  dplyr::select(!c("SetID")) %>%
  dplyr::mutate(gsd = 1.1)

pkRatiometaData <- attr(exampleDataCovariates, "metaData")
pkRatiometaData <- pkRatiometaData[intersect(names(pkRatioData), names(pkRatiometaData))]

knitr::kable(head(pkRatioData), digits = 3)

ID	Age	Obs	Pred	Ratio	AgeBin	Sex	Country	SD	gsd
1	48	4.00	2.90	0.725	Adults	Male	Canada	0.693	1.1
2	36	4.40	5.75	1.307	Adults	Male	Canada	0.188	1.1
3	52	2.80	2.70	0.964	Adults	Male	Canada	0.984	1.1
4	47	3.75	3.05	0.813	Adults	Male	Canada	0.591	1.1
5	0	1.95	5.25	2.692	Peds	Male	Canada	0.443	1.1
6	48	2.45	5.30	2.163	Adults	Male	Canada	0.072	1.1

knitr::kable(metaData2DataFrame(pkRatiometaData), digits = 3)

	Age	Obs	Pred	Ratio	SD
dimension	Age	Clearance	Clearance	Ratio	Clearance
unit	yrs	dL/h/kg	dL/h/kg		dL/h/kg

2. Predicted vs Observed (`plotPredVsObs()`)

2.1 Basic Examples

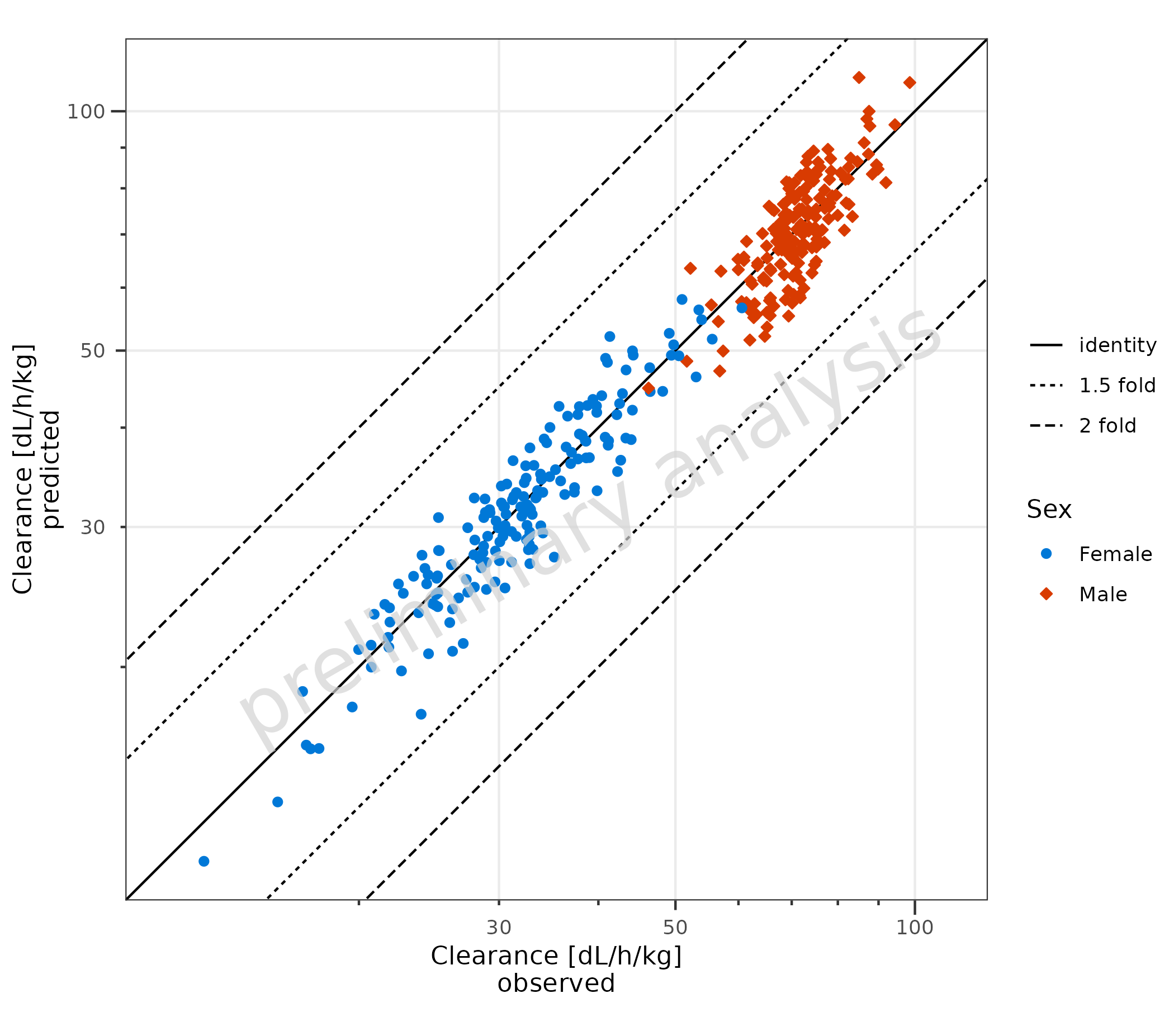
2.1.1 Default Settings

Basic example using default settings. Predicted and observed data are mapped with predicted and observed. The aesthetic groupby can be used to group observations.

plotPredVsObs(
  data = data,
  mapping = aes(
    observed = Obs,
    predicted = Pred,
    groupby = Sex
  ),
  metaData = metaData
)

Scatter plot showing predicted versus observed values with log-log scale. Points are colored by sex groups, with a unity line indicating perfect prediction. Most points cluster around the unity line indicating good model performance.

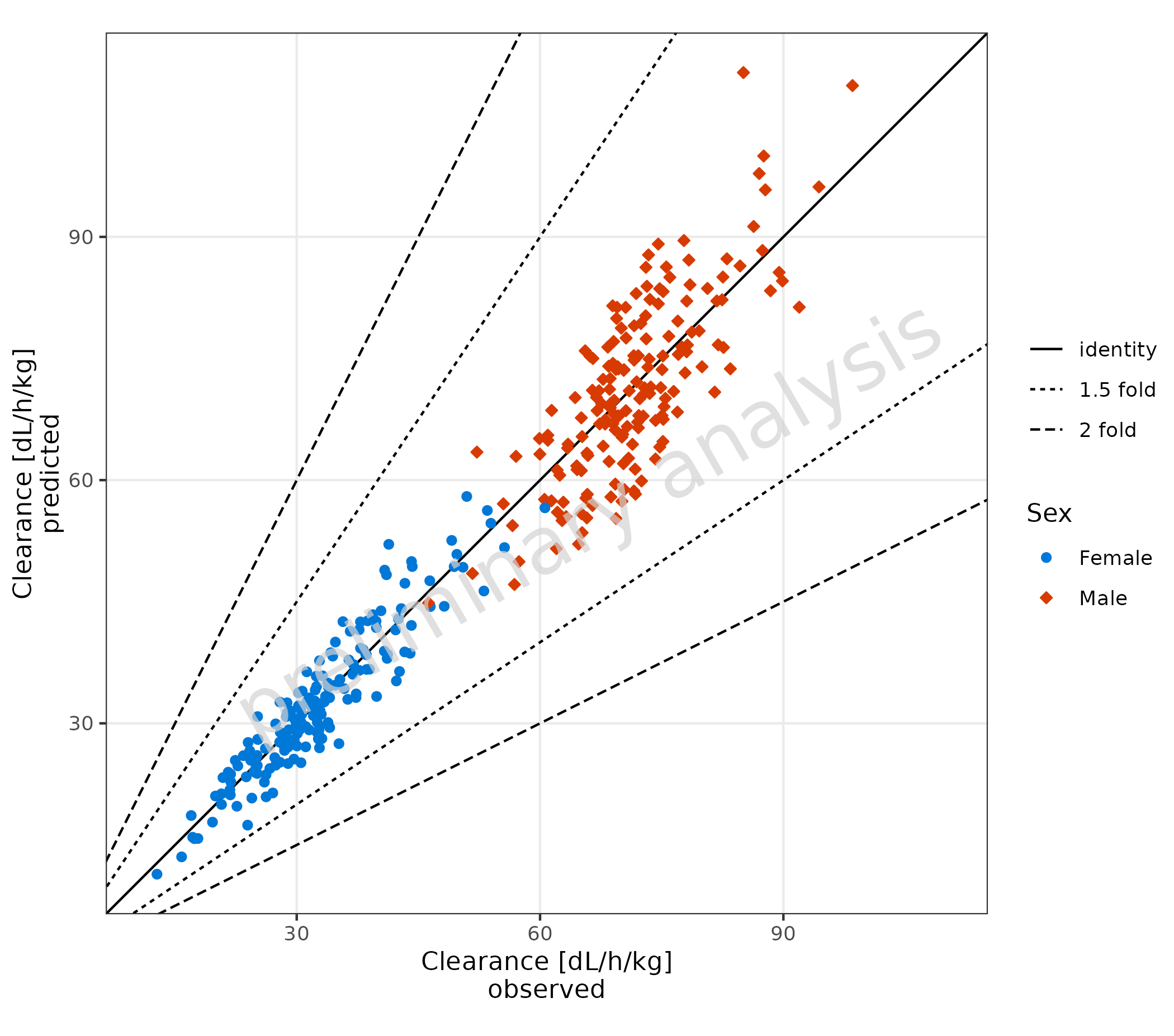
2.1.2 Basic Example: Linear Scale

The scale for the x and y axes is set to linear. It is not intended to use different scales for the x and y axes. Therefore, only one variable xyscale exists for both axes.

Predicted and observed data are mapped with x and y.

plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  xyscale = "linear"
)

Scatter plot showing predicted versus observed values with linear scale on both axes. Points are colored by sex groups with a unity line for reference. The linear scale allows for easier interpretation of absolute differences between predictions and observations.

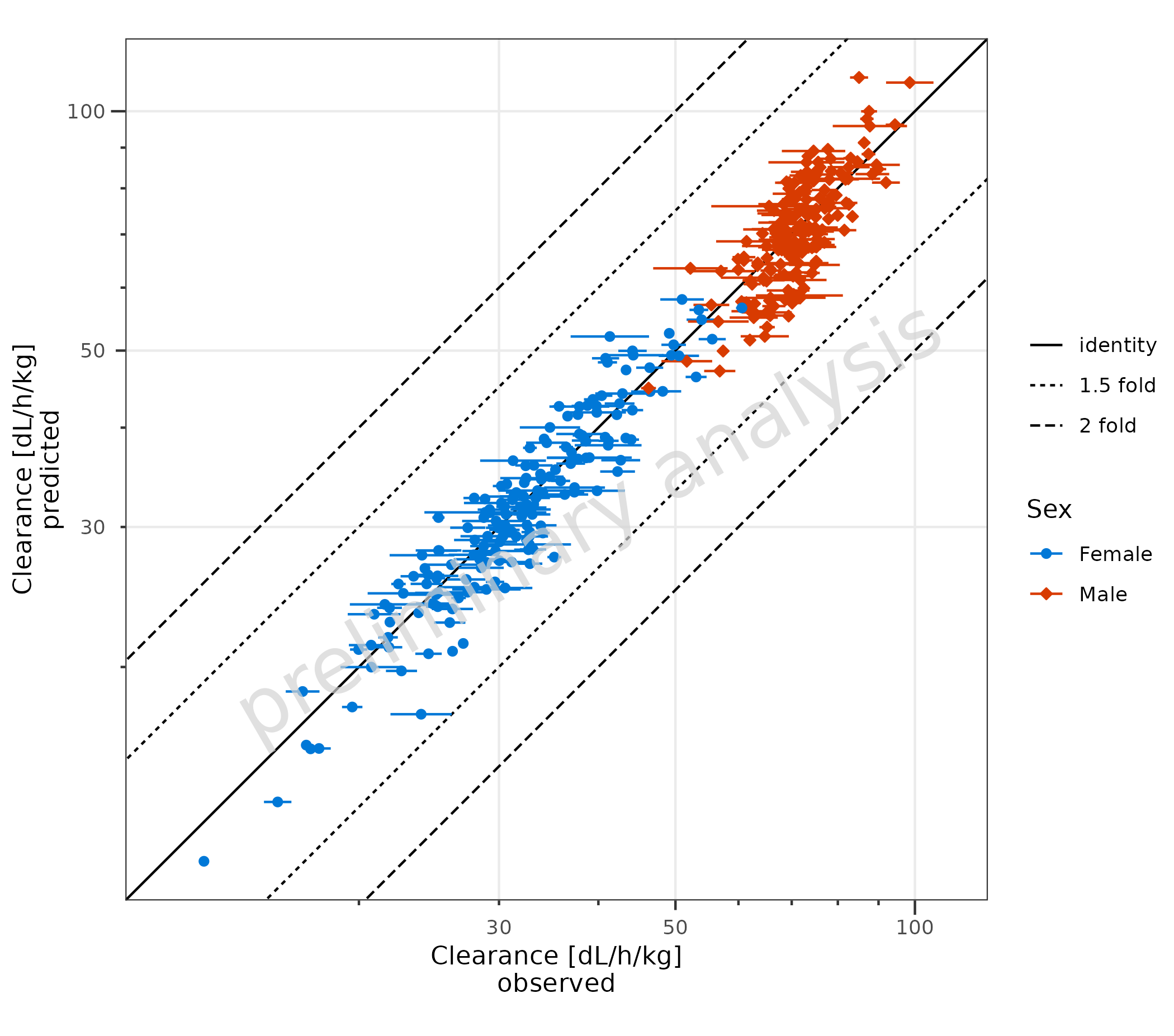
2.1.3 Error Bars for Observed Data

Error bars for the observed data are plotted. In the example, this is done by mapping error_relative. Error bars could also be produced by mapping error to a column with an additive error or mapping xmin and xmax explicitly.

plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    error_relative = gsd,
    groupby = Sex
  ),
  metaData = metaData
)

Scatter plot showing predicted versus observed values with horizontal error bars representing relative error in observed data. Points are colored by sex groups, and error bars show the uncertainty in the observed measurements.

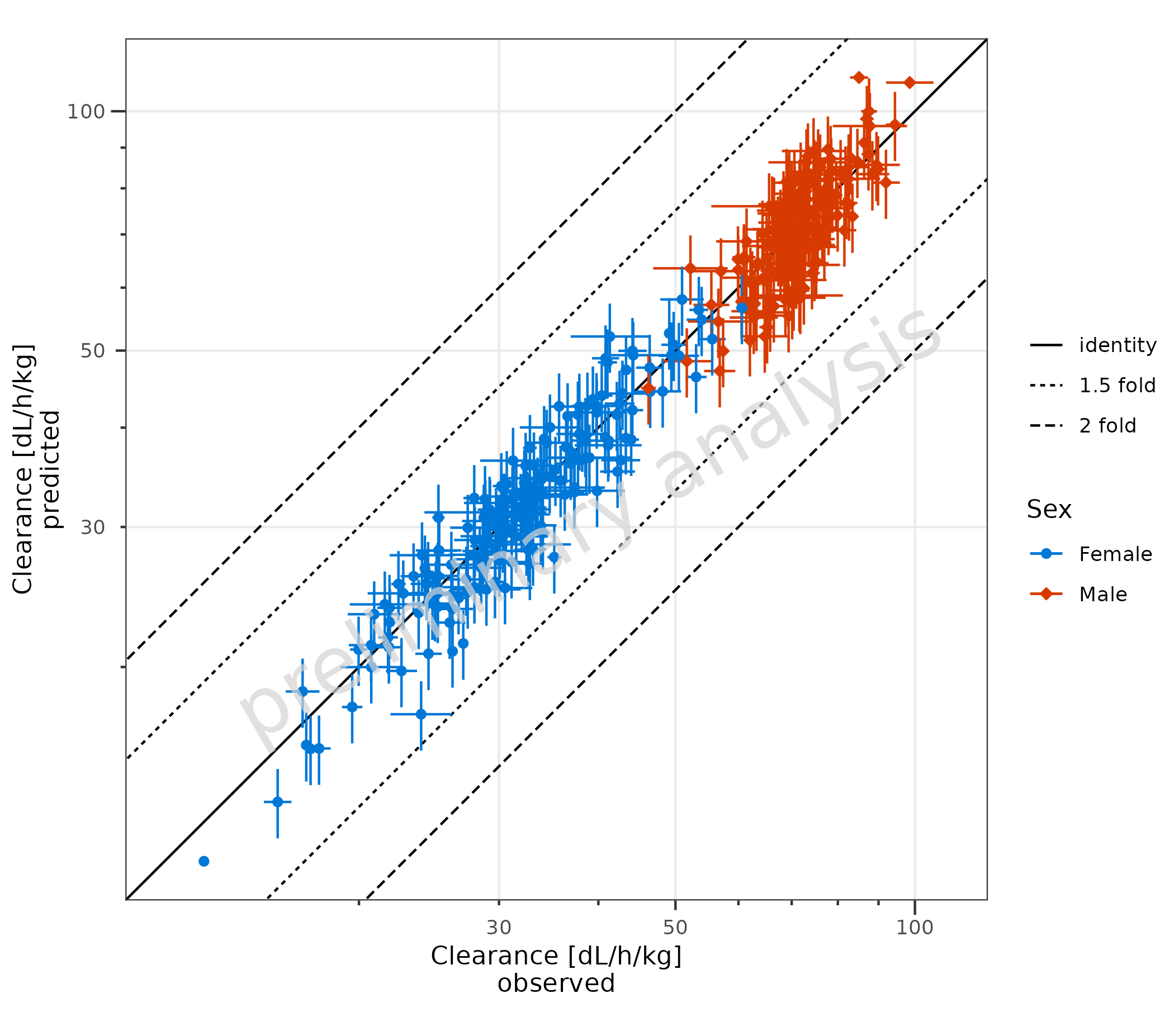
2.1.4 Error Bars for Observed and Predicted Data

To plot the prediction error, ymin and ymax must also be mapped explicitly.

plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    error_relative = gsd,
    ymin = Pred * 0.9,
    ymax = Pred * 1.1,
    groupby = Sex
  ),
  metaData = metaData
)

Scatter plot showing predicted versus observed values with both horizontal error bars (for observed data uncertainty) and vertical error bars (for predicted data uncertainty). Points are colored by sex groups, demonstrating how to display uncertainty in both measurements.

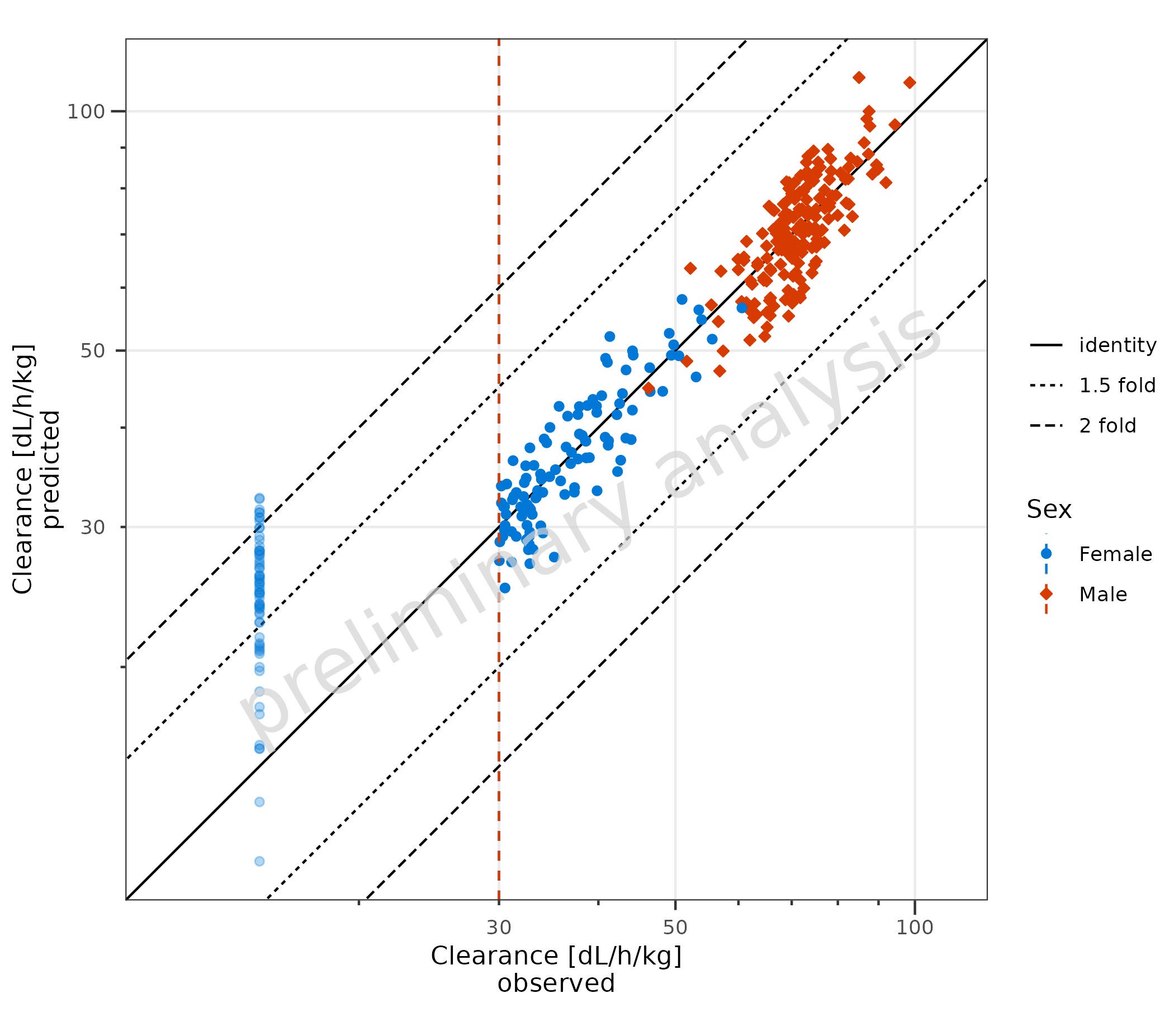
2.1.5 Example with LLOQ

Below, a dataset is created where the LLOQ is set to the 0.1 quantile of the observed data. All values below are set to LLOQ/2. By mapping lloq, these data are displayed with a lighter alpha, and a horizontal line for the LLOQ is added.

lloqData <- signif(quantile(data$Obs, probs = 0.1), 1)

dataLLOQ <- data %>%
  dplyr::mutate(lloq = lloqData) %>%
  dplyr::mutate(Obs = ifelse(Obs <= lloq, lloq / 2, Obs))

plotPredVsObs(
  data = dataLLOQ,
  mapping = aes(
    x = Obs,
    y = Pred,
    lloq = lloq,
    groupby = Sex
  ),
  metaData = metaData
)

Scatter plot showing predicted versus observed values with lower limit of quantification (LLOQ) handling. Values below the LLOQ are displayed with reduced transparency and marked with a horizontal LLOQ line. Data points below LLOQ are set to LLOQ/2 for visualization.

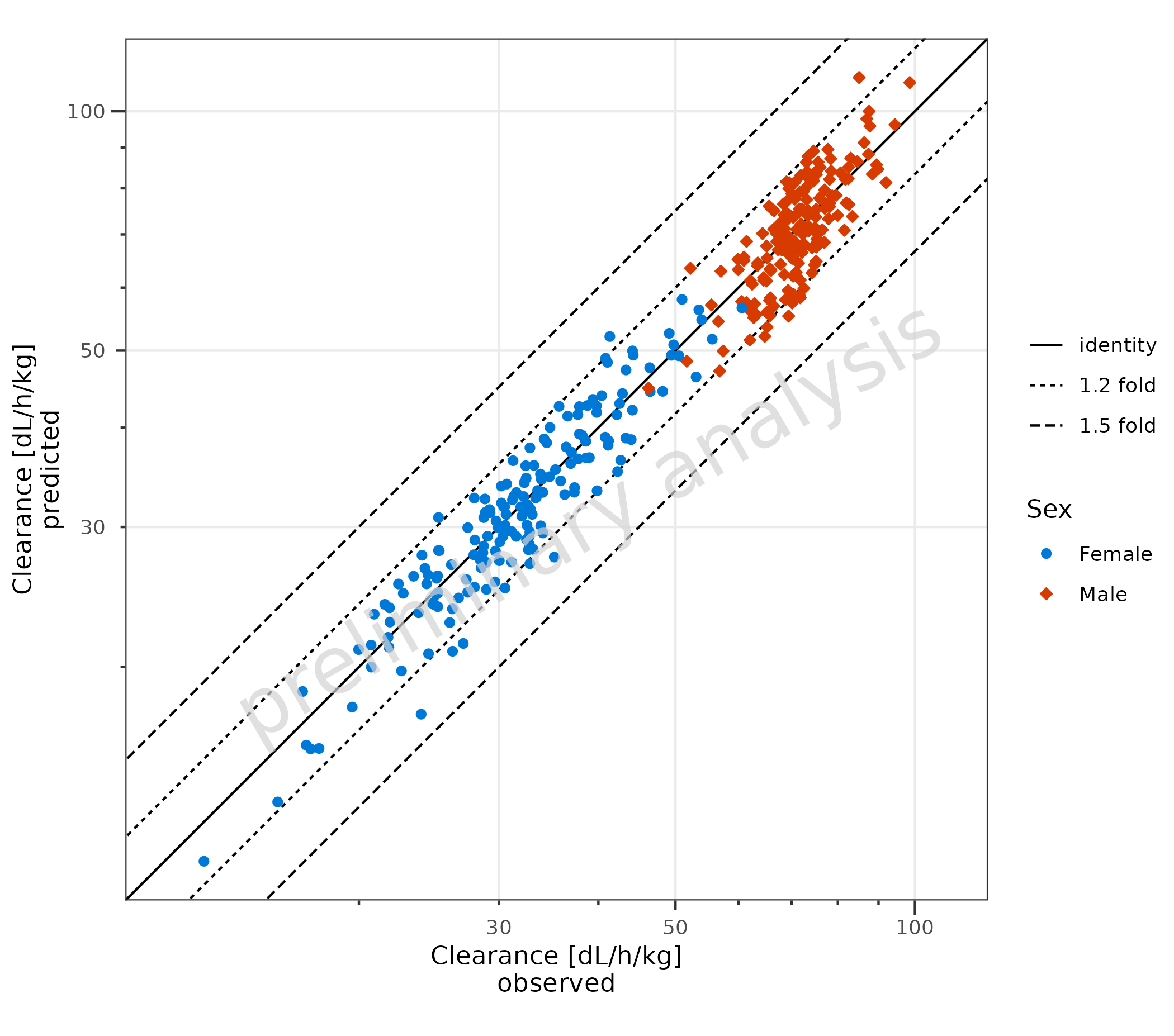
2.2 Adjust Comparison Lines

2.2.1 Adjust Fold Distance

plotPredVsObs() adds lines to indicate fold distances. The lines are defined by the variable comparisonLineVector, which is a named list with default values list(identity = 1, '1.5 fold' = c(1.5, 1/1.5), '2 fold' = c(2, 1/2)).

A fold distance list can be generated by the helper function ?getFoldDistanceList().

Below, the 1.2 and 1.5 distances are displayed:

plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  comparisonLineVector = getFoldDistanceList(c(1.2, 1.5))
)

Scatter plot showing predicted versus observed values with custom fold distance lines. The plot includes 1.2-fold and 1.5-fold comparison lines around the unity line, helping to assess the degree of prediction accuracy. Points are colored by sex groups.

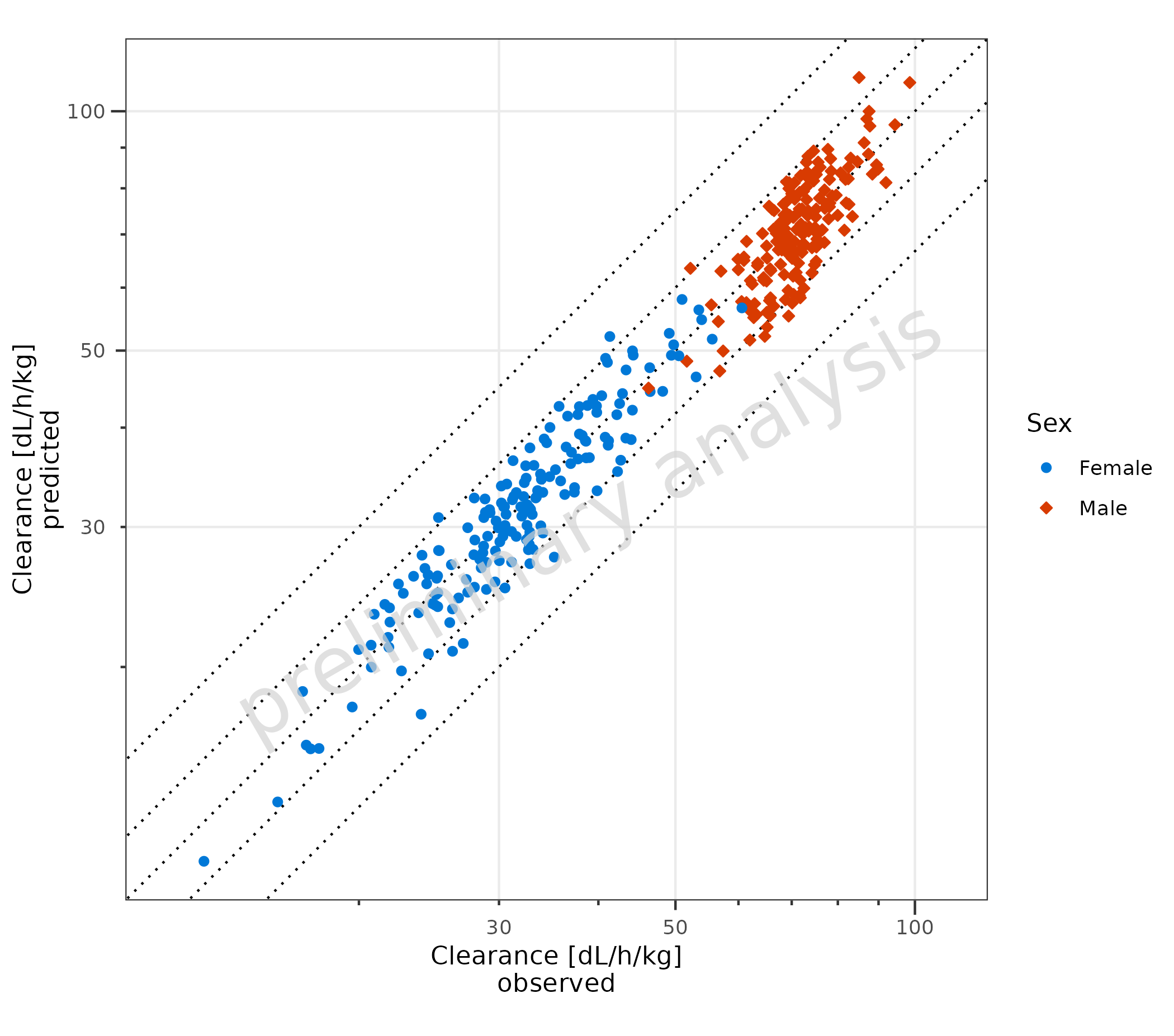
2.2.2 Adjust Display of Lines

The names of the list are displayed in the legend.

If the list is unnamed, all lines are displayed with the same line type, and they are not included in the legend. The line type used is settable by the variable geomComparisonLineAttributes.

If the variable comparisonLineVector is NULL, no lines will be displayed.

plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  comparisonLineVector = unname(getFoldDistanceList(c(1.2, 1.5))),
  geomComparisonLineAttributes = list(linetype = "dotted")
)

Scatter plot showing predicted versus observed values with unnamed fold distance lines displayed as dotted lines. The fold lines are shown without legend entries and all use the same dotted line style for a cleaner appearance. Points are colored by sex groups.

2.3 Adding a Regression Line

To add a regression line, set the input variable addRegression to TRUE (A). For regression lines, the package ggpubr has a function stat_regline_equation to add statistics of the regression as labels (B). To use other functions, e.g., local polynomial regression, use ggplot2::geom_smooth directly (C).

# A
plotObject <- plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  addRegression = TRUE
) +
  labs(title = "Regression Line", tag = "A")

plot(plotObject)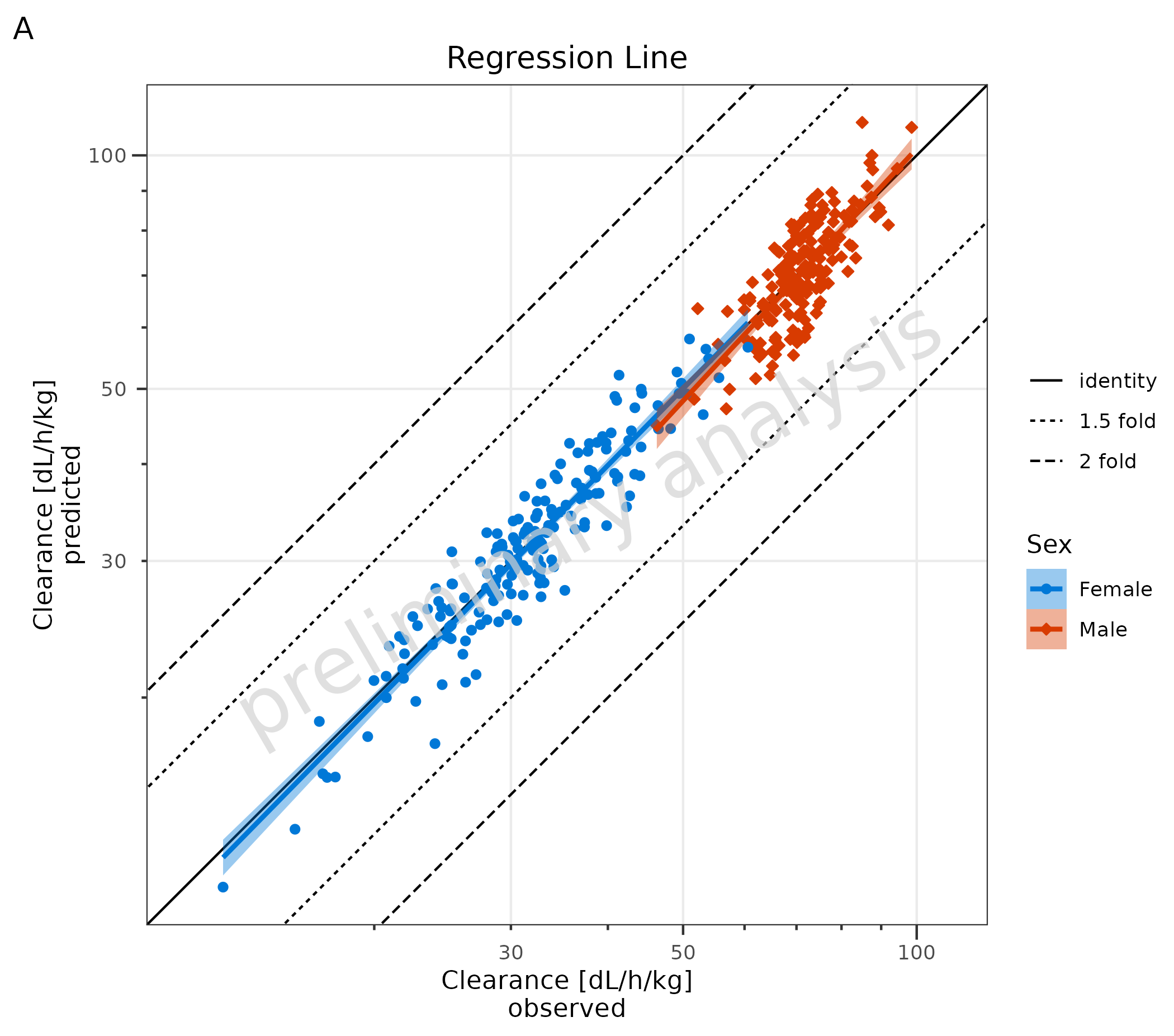

Scatter plot showing predicted versus observed values with linear regression line overlay. Points are colored by sex groups, and a fitted regression line shows the overall trend with confidence intervals. The plot demonstrates the relationship between predicted and observed values beyond the unity line.

# B
plotObject + ggpubr::stat_regline_equation(aes(label = after_stat(rr.label))) + labs(title = "With RR as Label", tag = "B")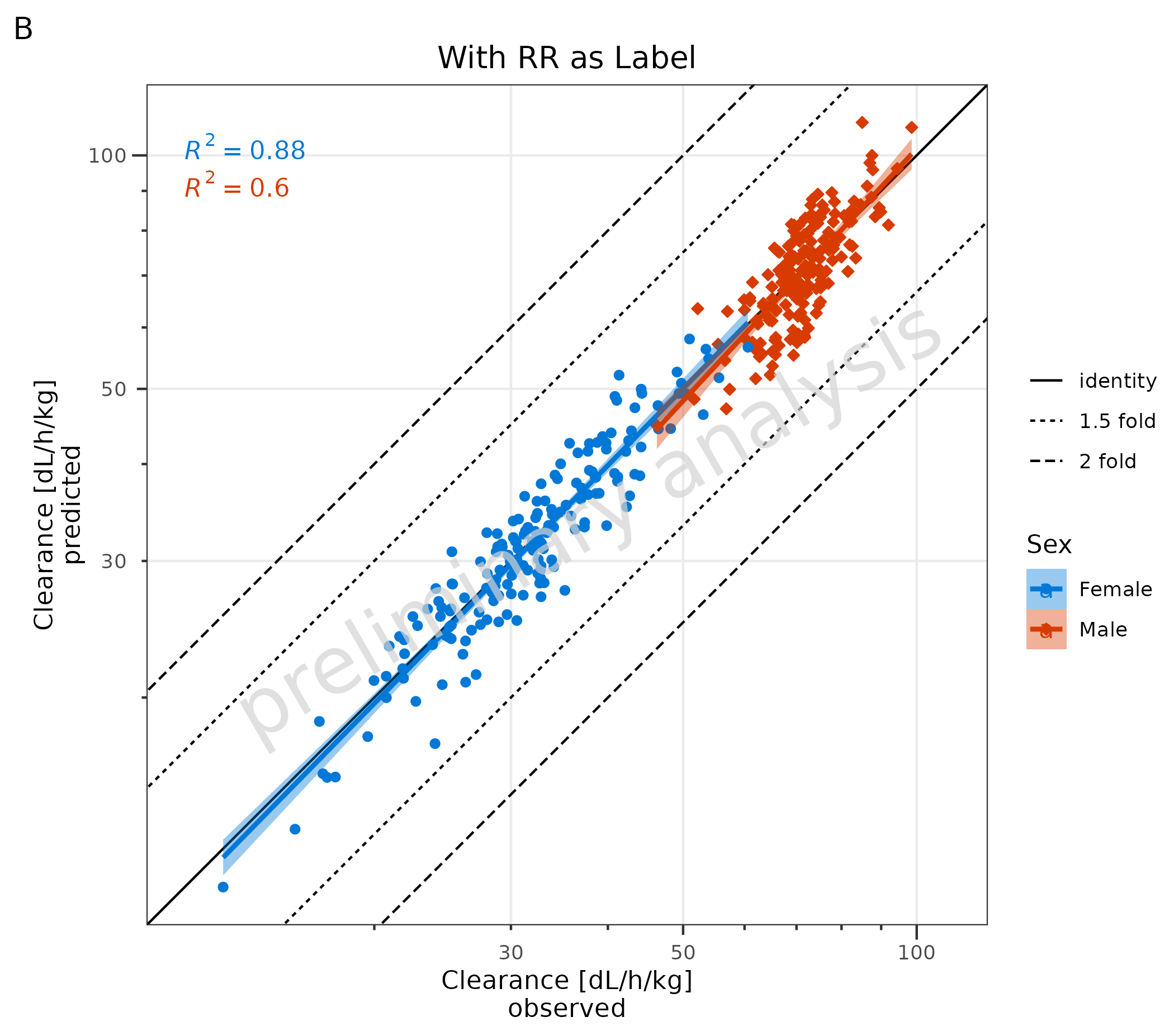

Scatter plot showing predicted versus observed values with linear regression line and R-squared statistics displayed. The plot includes the regression line with confidence intervals and an overlaid R-squared label showing the goodness of fit. Points are colored by sex groups.

# C Local Polynomial Regression Fitting
plotPredVsObs(
  data = data,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  addRegression = FALSE
) +
  geom_smooth(method = "loess", formula = "y ~ x", na.rm = TRUE) +
  labs(title = "Local Polynomial Regression Fitting", tag = "C")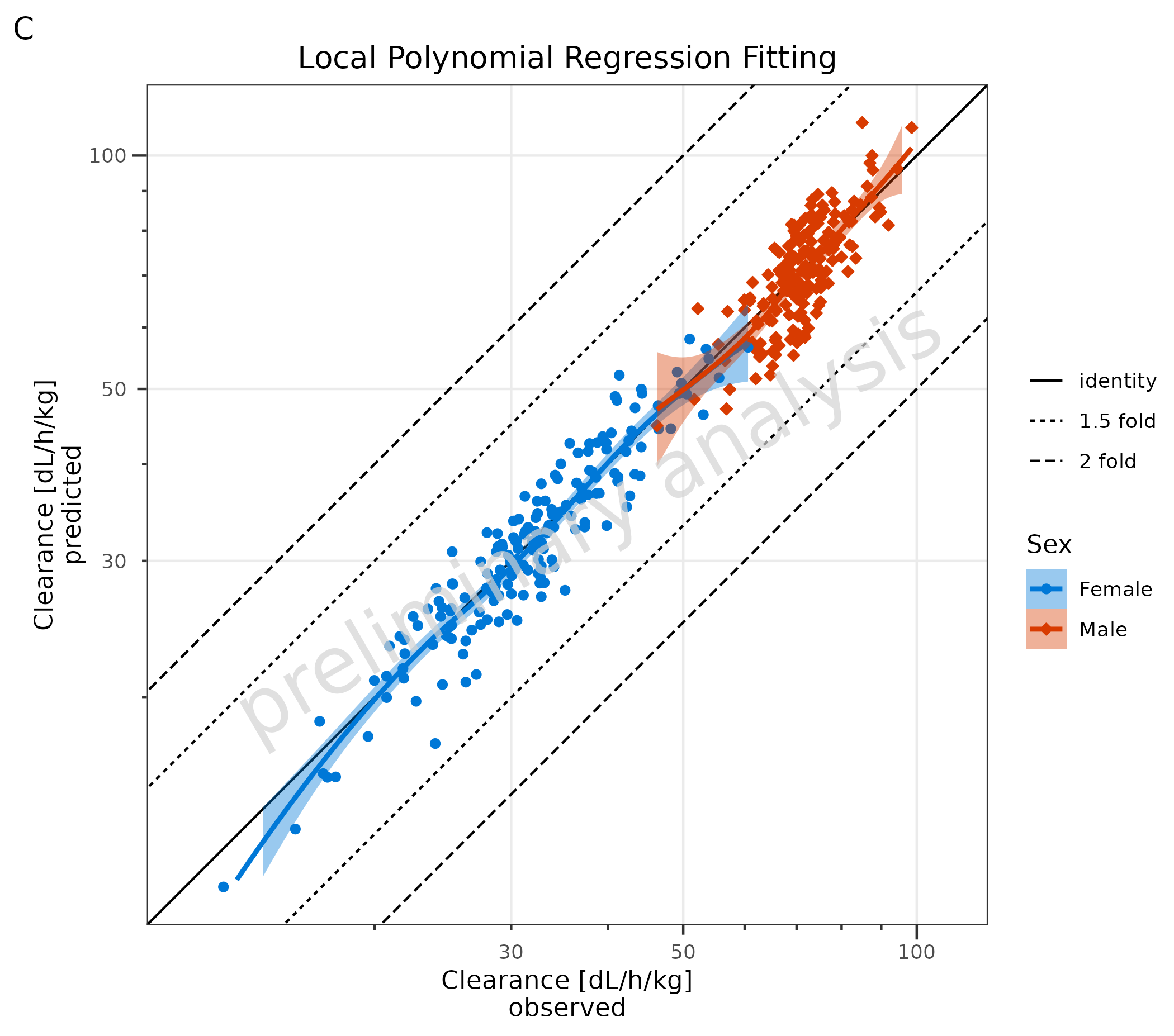

Scatter plot showing predicted versus observed values with local polynomial regression (LOESS) smoothing. The curved fitted line with confidence intervals captures non-linear patterns in the data that a linear regression might miss. Points are colored by sex groups.

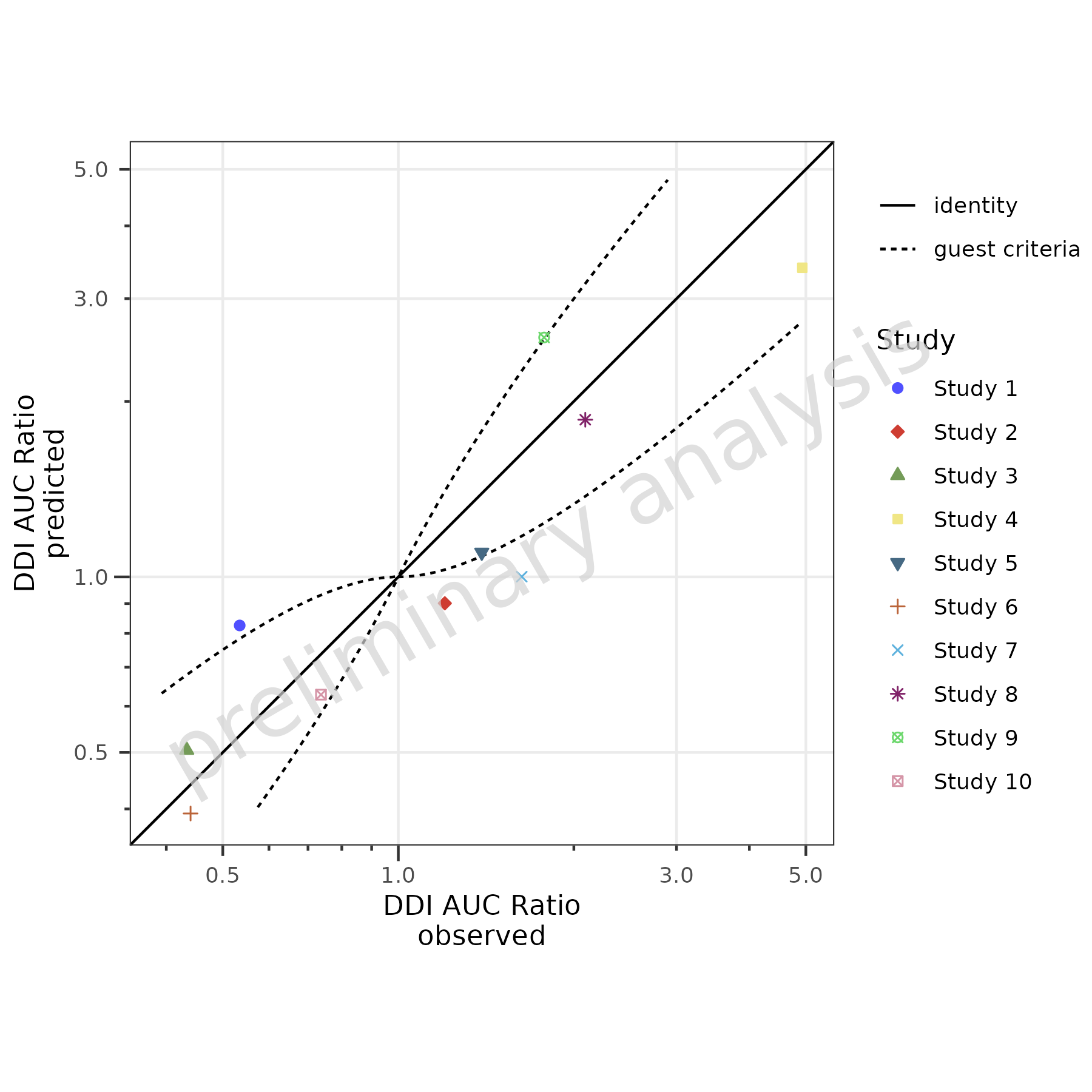
2.4 Add Guest Criteria Lines

To compare DDI ratios, set the variable addGuestLimits to TRUE and set the variable deltaGuest:

plotPredVsObs(
  data = dDIdata,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Study
  ),
  metaData = dDImetaData,
  addGuestLimits = TRUE,
  comparisonLineVector = list(identity = 1),
  deltaGuest = 1
)

Square scatter plot showing predicted versus observed DDI ratios with Guest criteria lines for drug-drug interaction assessment. The plot includes Guest limit lines that define acceptable ranges for DDI predictions, with different studies shown in different colors. The square format ensures equal scaling for both axes.

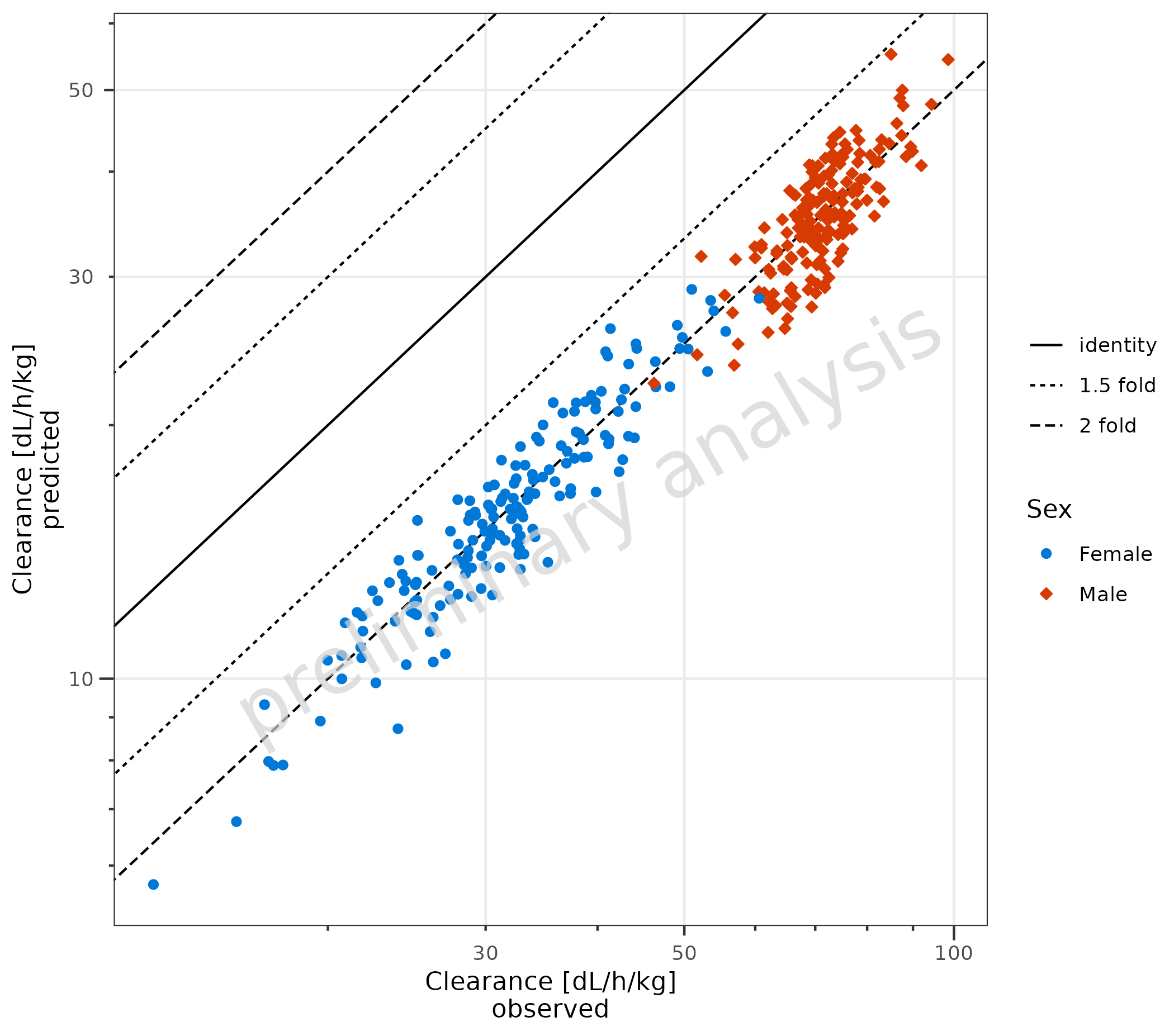
2.5 Use Non-Square Format

By default, plotPredVsObs() produces a square plot with an aspect ratio of 1 and the same limits for the x and y axes. In the example below, the Predicted values are set to 1/2 of the original values. A square plot does not make sense anymore; therefore, the variable asSquarePlot is set to FALSE.

dataNonSquare <- data %>%
  dplyr::mutate(Pred = Pred / 2)

plotPredVsObs(
  data = dataNonSquare,
  mapping = aes(
    x = Obs,
    y = Pred,
    groupby = Sex
  ),
  metaData = metaData,
  asSquarePlot = FALSE
)

Non-square scatter plot showing predicted versus observed values where predicted values have been scaled to half of observed values. The plot demonstrates how to handle cases where data ranges differ significantly between axes, using non-square format for better visualization. Points are colored by sex groups.

3. Residuals vs Covariate (`plotResVsCov()`)

3.1 Basic Examples

The function plotResVsCov() calculates the residuals using the aesthetics observed and predicted.

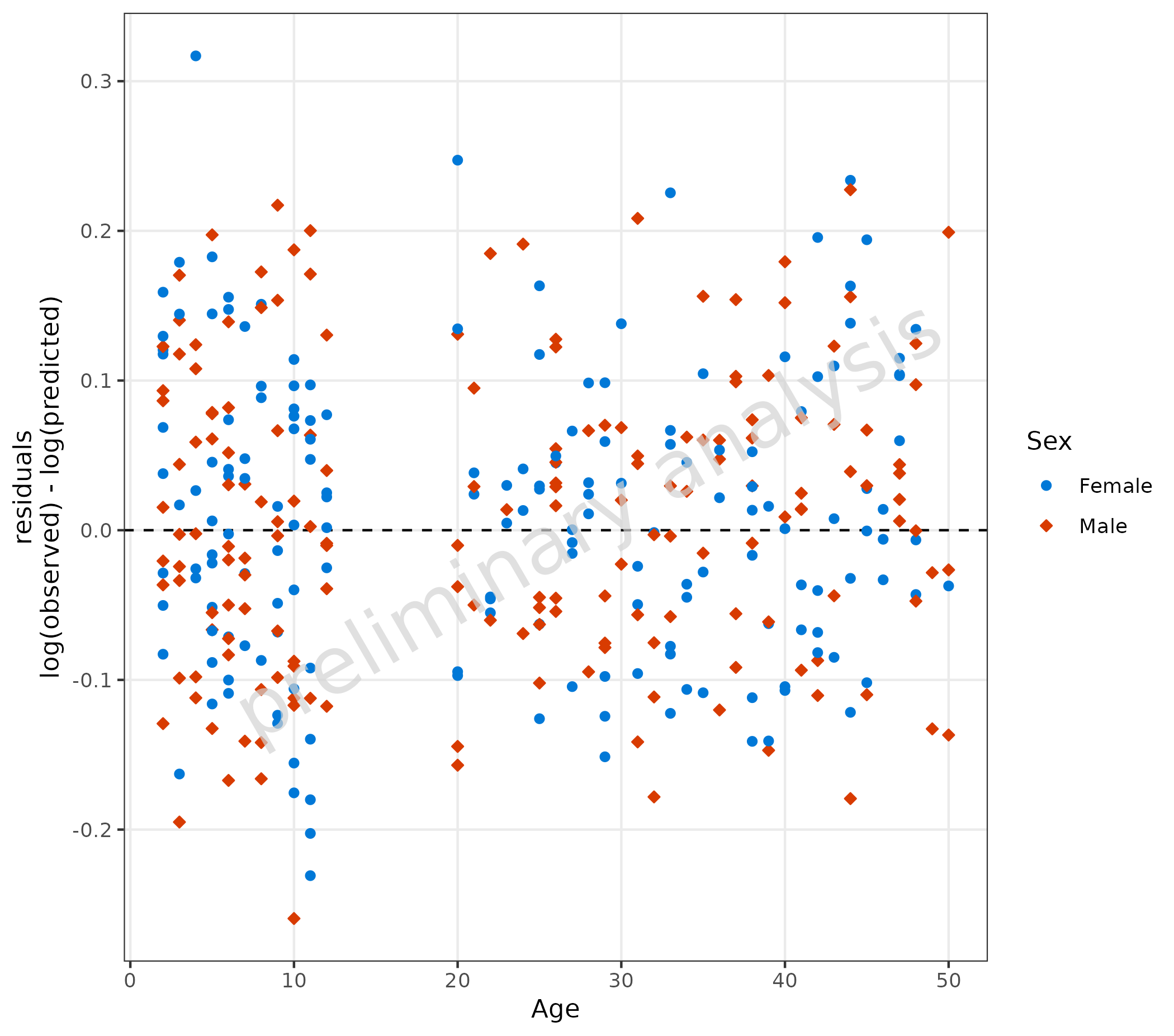
3.1.1 Default Settings

The default value for the variable residualScale is “log”. Residuals will then be calculated by log(observed) - log(predicted). A horizontal comparison line with the value 0 is displayed. The aesthetic groupby can be used to group observations.

plotResVsCov(
  data = data,
  mapping = aes(
    x = Age,
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  )
)

Scatter plot showing log residuals versus age with default settings. Residuals are calculated as log(observed) - log(predicted), displayed as points colored by sex groups. A horizontal reference line at zero indicates perfect prediction. Points scattered around zero suggest good model performance.

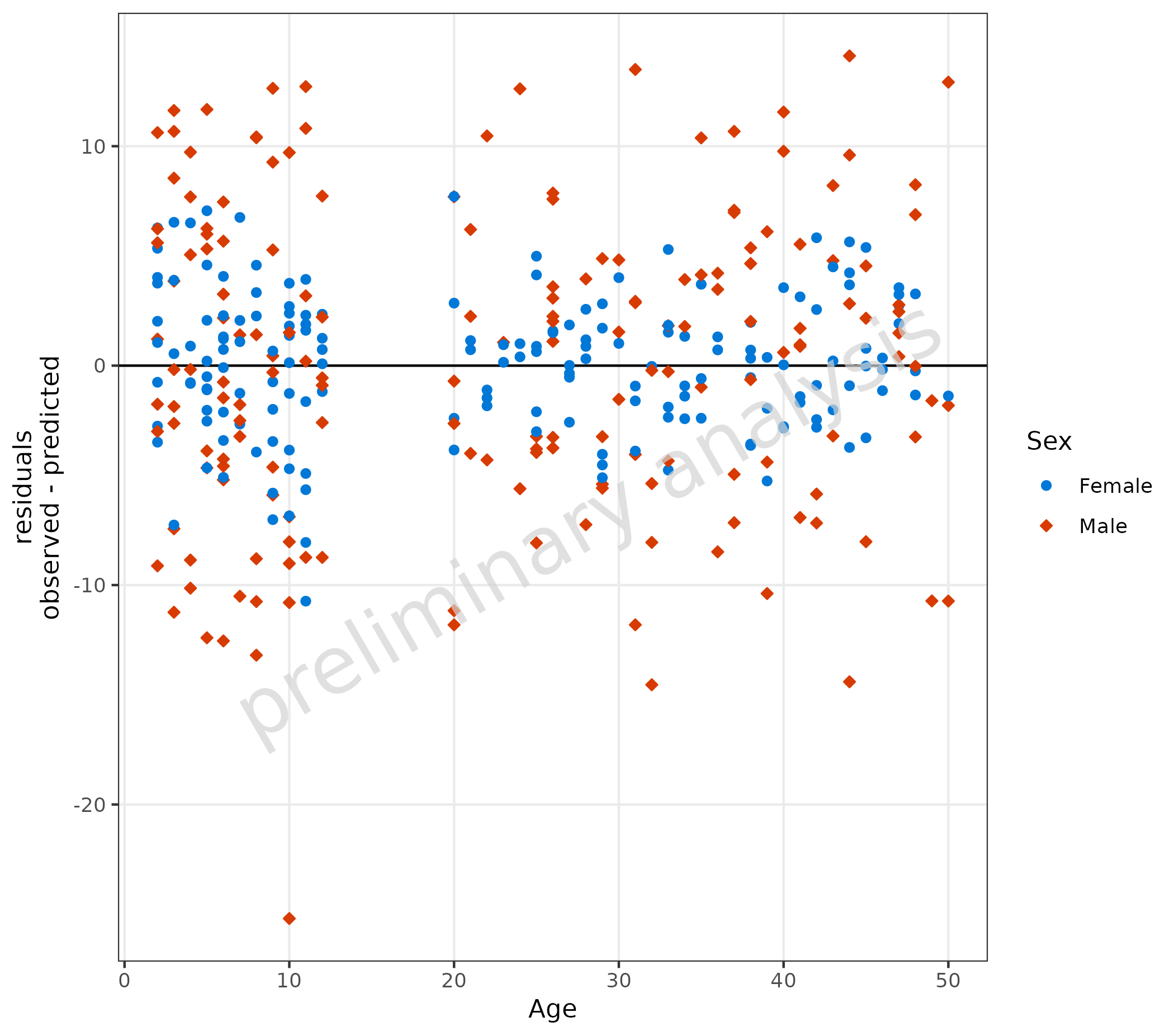
3.1.2 Linear Scale for Residuals

If the variable residualScale is set to “linear”, residuals will be calculated by #$# observed - predicted #$#.

Below, the line type of the comparison line is set to ‘solid’.

plotResVsCov(
  data = data,
  mapping = aes(
    x = Age,
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  ),
  residualScale = "linear",
  geomComparisonLineAttributes = list(linetype = "solid")
)

Scatter plot showing linear residuals versus age with a solid horizontal reference line. Residuals are calculated as observed - predicted on a linear scale, with points colored by sex groups. The solid reference line at zero provides a clear visual reference for assessing prediction accuracy.

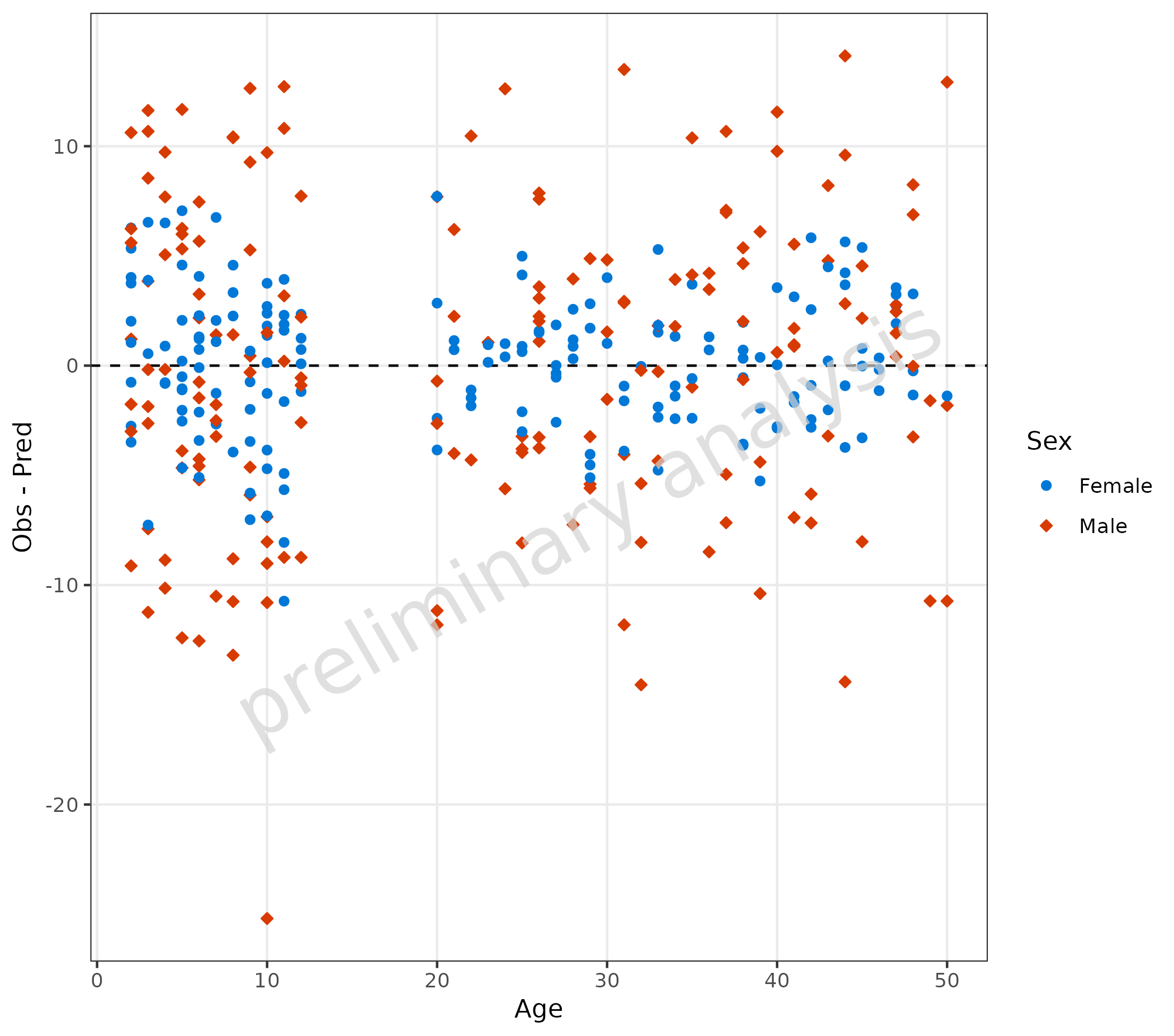
3.1.3 Map Residuals Directly

It is also possible to use already calculated residuals or formulas by using the aesthetic ‘y’.

plotResVsCov(
  data = data,
  mapping = aes(
    x = Age,
    y = Obs - Pred,
    groupby = Sex
  )
)

Scatter plot showing directly calculated residuals (observed minus predicted) versus age. Residuals are manually calculated and mapped to the y-axis, with points colored by sex groups. This demonstrates how to use pre-calculated residuals instead of automatic calculation.

3.2 Adjusting Comparison Lines

plotResVsCov(
  data = data,
  mapping = aes(
    x = Age,
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  ),
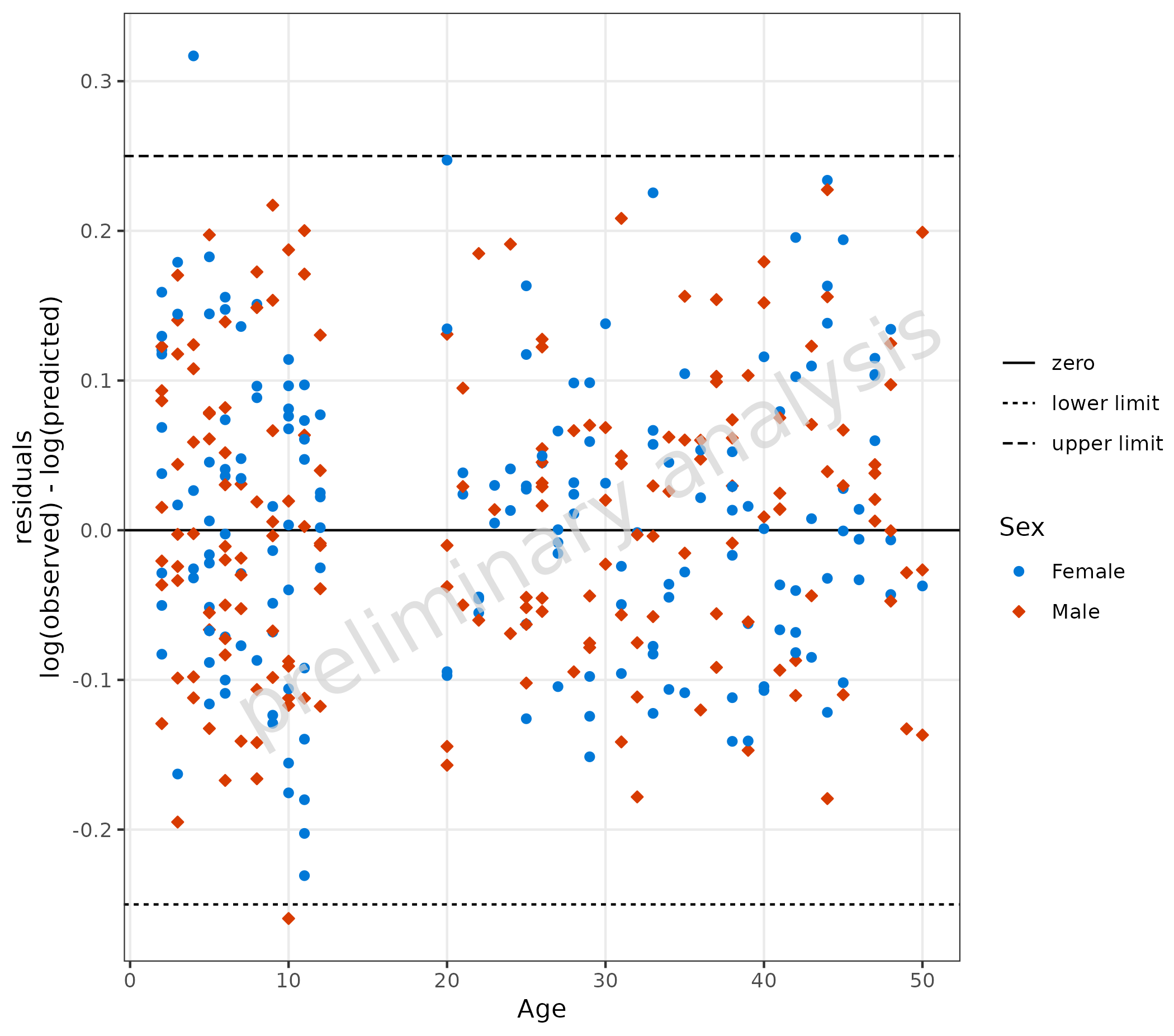
  comparisonLineVector = list(zero = 0, "lower limit" = -0.25, "upper limit" = 0.25)
)

Scatter plot showing residuals versus age with custom comparison lines. The plot includes a zero reference line and additional upper and lower limit lines at ±0.25, providing multiple reference points for evaluating prediction accuracy. Points are colored by sex groups.

3.3 Adding a Regression Line

To add a regression line, set the input variable addRegression to TRUE. For regression lines, the package ggpubr has a nice function stat_regline_equation to add statistics of the regression as labels.

plotResVsCov(
  data = data,
  mapping = aes(
    x = Age,
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  ),
  addRegression = TRUE
) +
  ggpubr::stat_regline_equation(aes(label = after_stat(eq.label)))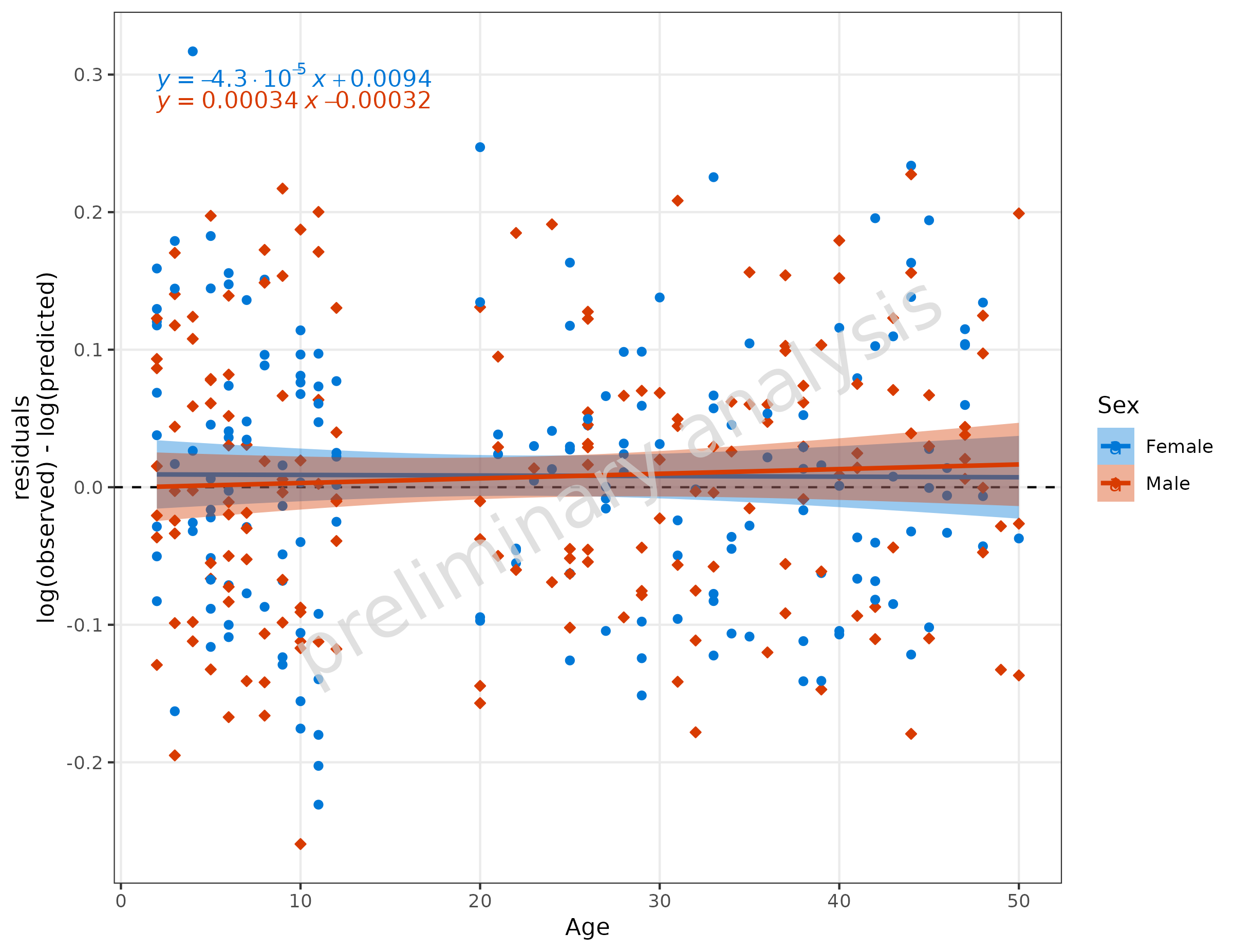

Scatter plot showing residuals versus age with linear regression line and equation overlay. The plot includes both a fitted regression line and the regression equation statistics, helping to identify any systematic bias in residuals with respect to age. Points are colored by sex groups.

4. Ratio Plots (`plotRatioVsCov()`)

4.1 Basic Examples

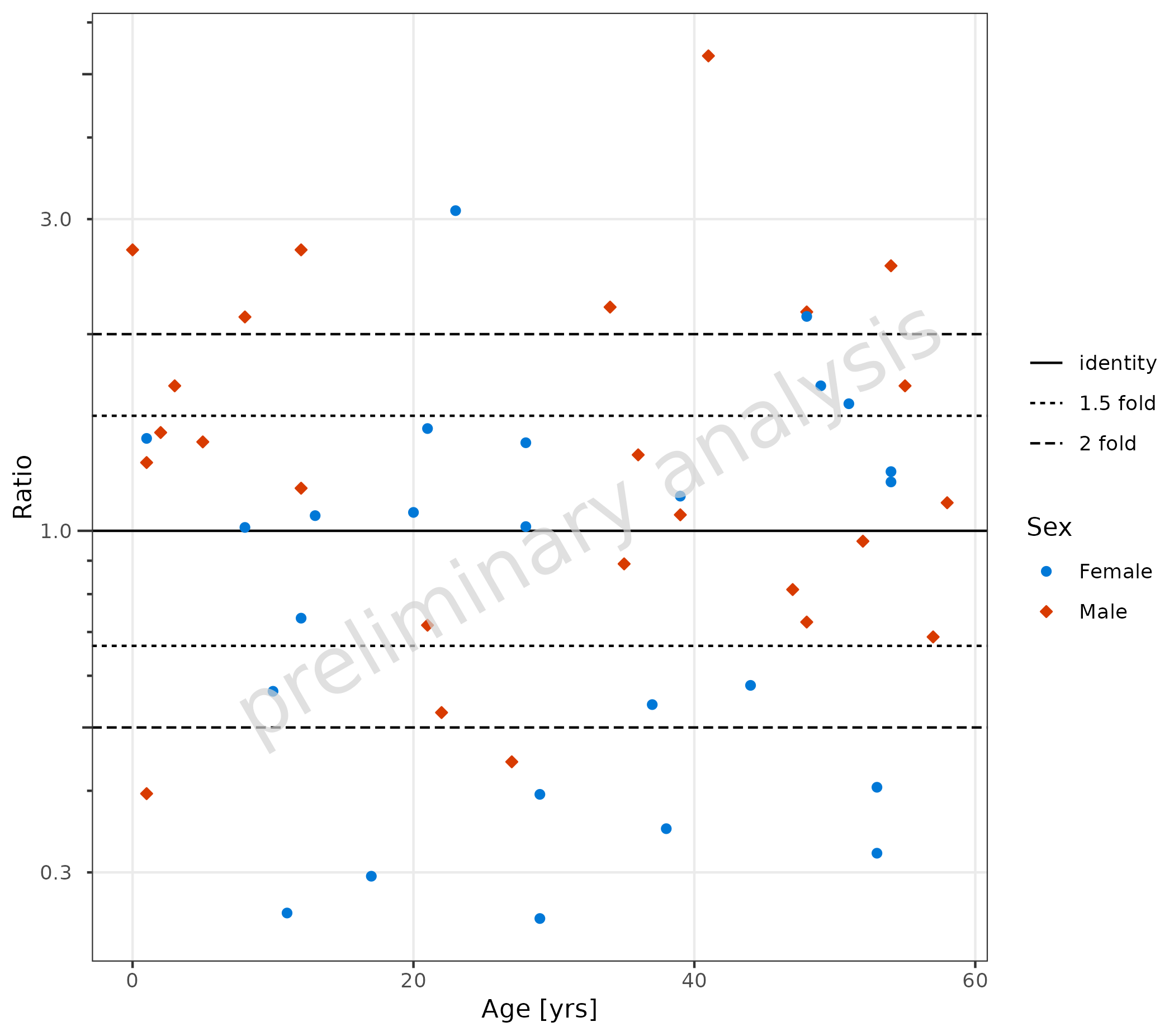
4.1.1 Default Settings

plotRatioVsCov() is used to evaluate ratios versus a covariate. By default, the identity and 1.5 and 2 point lines are added, and the default for yscale is ‘log’. The aesthetic groupby can be used to group observations.

plotRatioVsCov(
  data = pkRatioData,
  mapping = aes(
    x = Age,
    y = Ratio,
    groupby = Sex
  ),
  metaData = metaData
)

Log-scale scatter plot showing ratio values versus age with default comparison lines. The plot displays ratios with identity line at 1 and fold-distance lines at 1.5 and 2. Points are colored by sex groups, with the log scale helping to visualize multiplicative relationships.

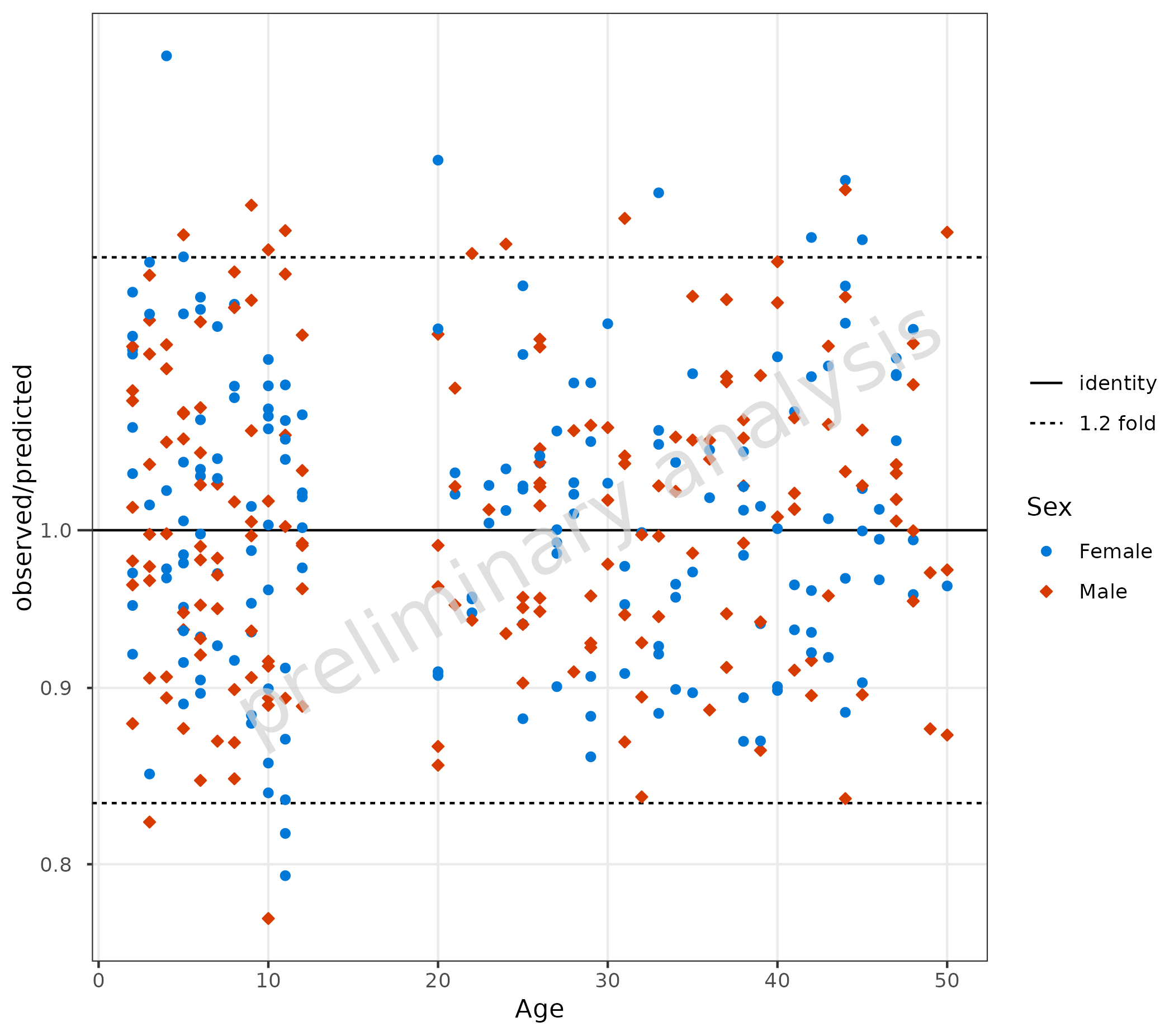
4.1.2 Compare Residuals as Ratio

Within the function plotRatioVsCov(), the variable residualScale is fixed to “ratio”, and the ratio of the residuals is calculated as $ observed / predicted $. Below, the comparison line is set to a 1.2 fold distance.

plotRatioVsCov(
  data = data,
  mapping = aes(
    x = Age,
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  ),
  comparisonLineVector = getFoldDistanceList(c(1.2))
)

Scatter plot showing residual ratios (observed/predicted) versus age with 1.2-fold comparison lines. The plot demonstrates ratio-based residual analysis, where ratios above or below the comparison lines indicate systematic over- or under-prediction. Points are colored by sex groups.

4.1.3 Using `{ospsuite.plots}` Specific Aesthetics like MDV and `error_relative`

If some of the data should be omitted, we can do this by mapping a logical column to the aesthetic mdv. Below, we exclude data with Age less than 20.

Additional error bars are displayed by mapping the column “gsd” to the aesthetic error_relative.

plotRatioVsCov(
  data = pkRatioData,
  mapping = aes(
    x = Age,
    y = Ratio,
    error_relative = gsd,
    mdv = Age < 20,
    groupby = Sex
  )
) + theme(legend.box = "horizontal", legend.title = element_blank())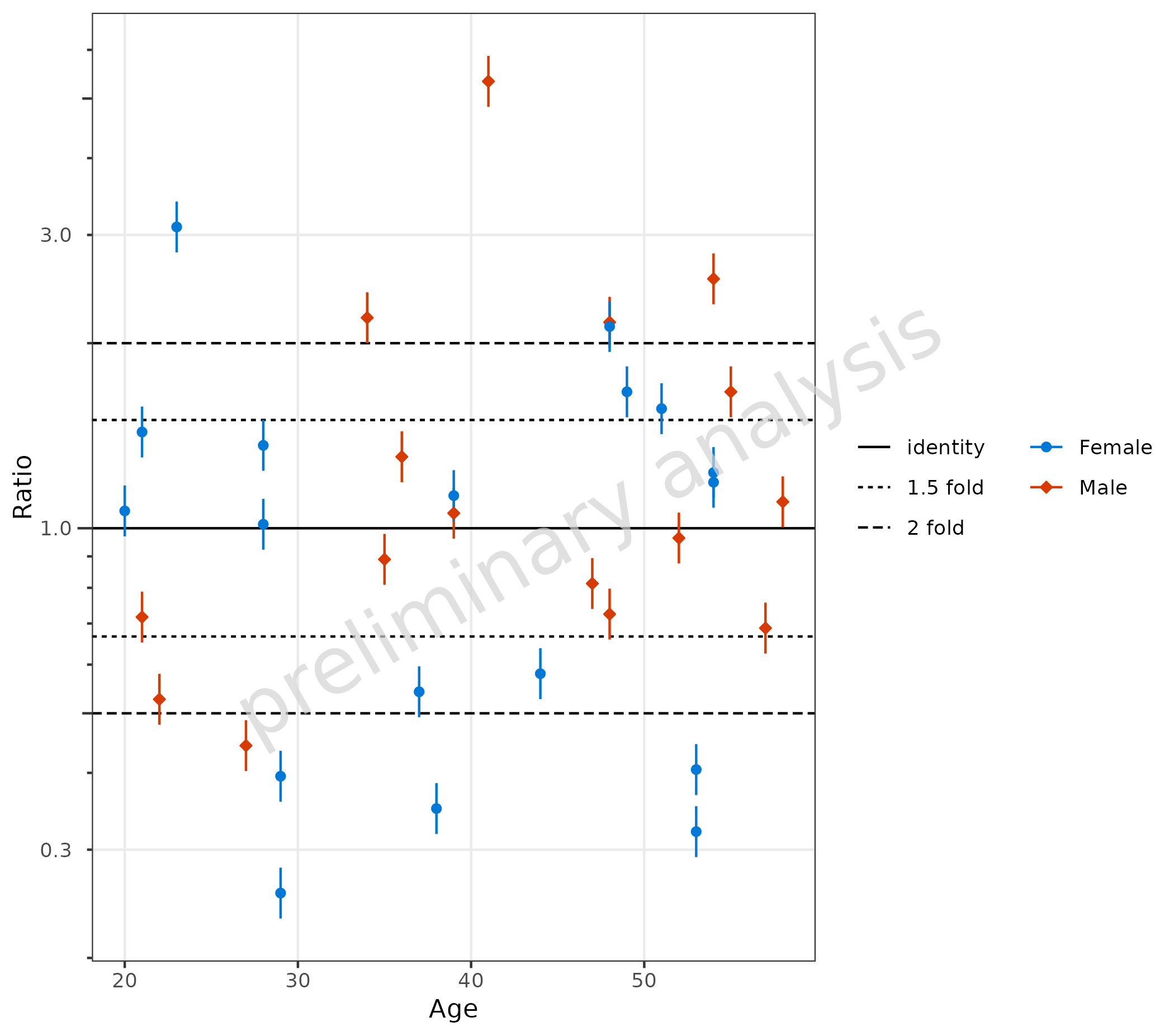

Scatter plot showing ratio values versus age with error bars and missing data exclusion. Data points with age less than 20 are excluded (MDV flag), and relative error bars show uncertainty in the measurements. Points are colored by sex groups with horizontal legend layout.

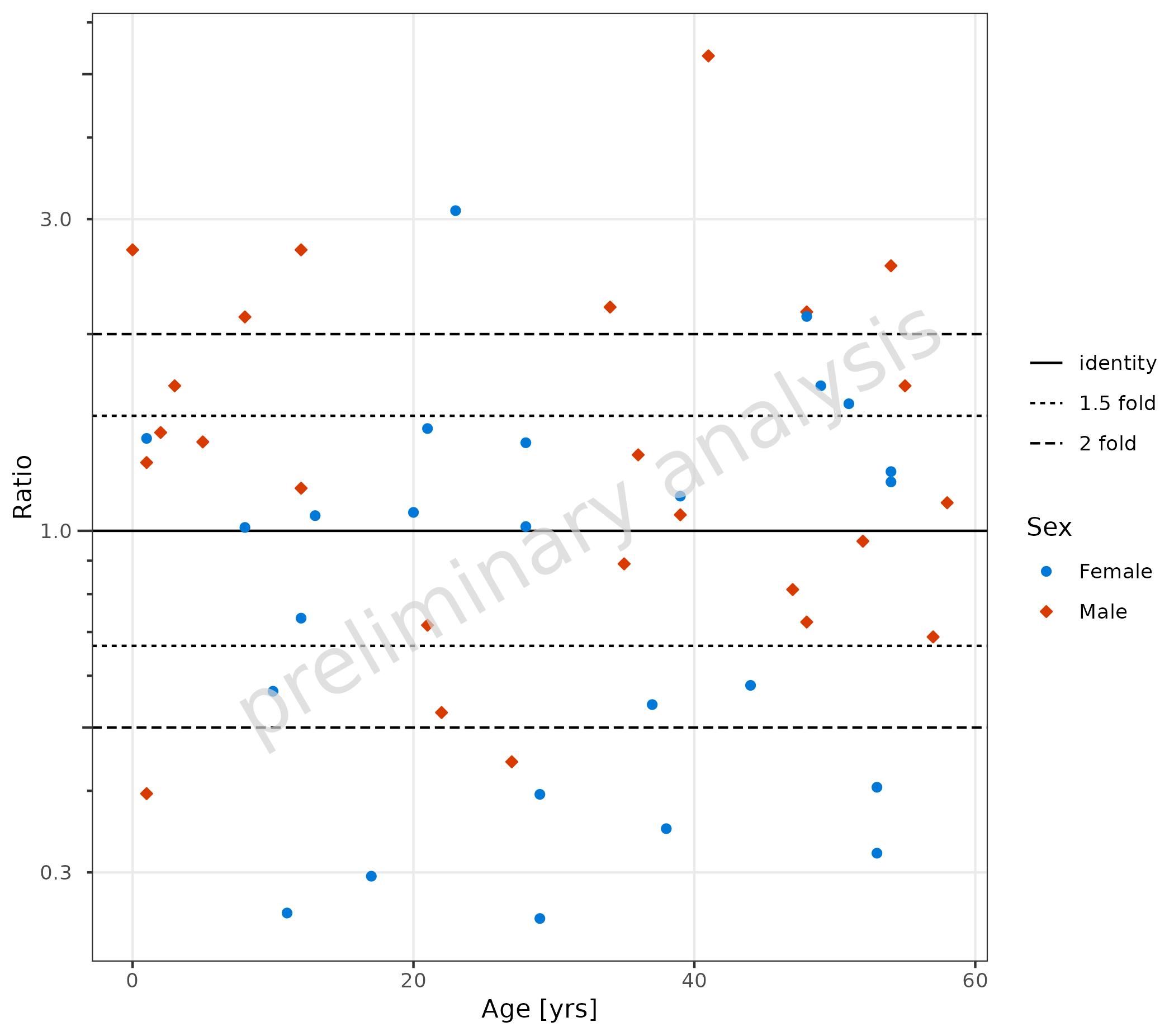
4.2 Qualification of Ratios

If the data.table package is installed and the variable comparisonLineVector is a named list, the {ggplot} object returned by plotRatioVsCov has an additional entry countsWithin, which contains a data.frame with the fractions within the specific ranges given by the variable comparisonLineVector.

plotObject <- plotRatioVsCov(
  data = pkRatioData,
  mapping = aes(
    x = Age,
    y = Ratio,
    groupby = Sex
  ),
  metaData = metaData
)

plot(plotObject)

knitr::kable(plotObject$countsWithin, caption = "Counts and fraction within ranges")

Counts and fraction within ranges
group	Points total	1.5 fold Number	1.5 fold Fraction	2 fold Number	2 fold Fraction
all Groups	50	24	0.48	32	0.64
Female	25	11	0.44	16	0.64
Male	25	13	0.52	16	0.64

$Scatter plot showing ratio values versus age with qualification analysis. The plot generates both the visualization and a statistical summary table showing the fraction of data points within specified comparison ranges. Points are colored by sex groups.$

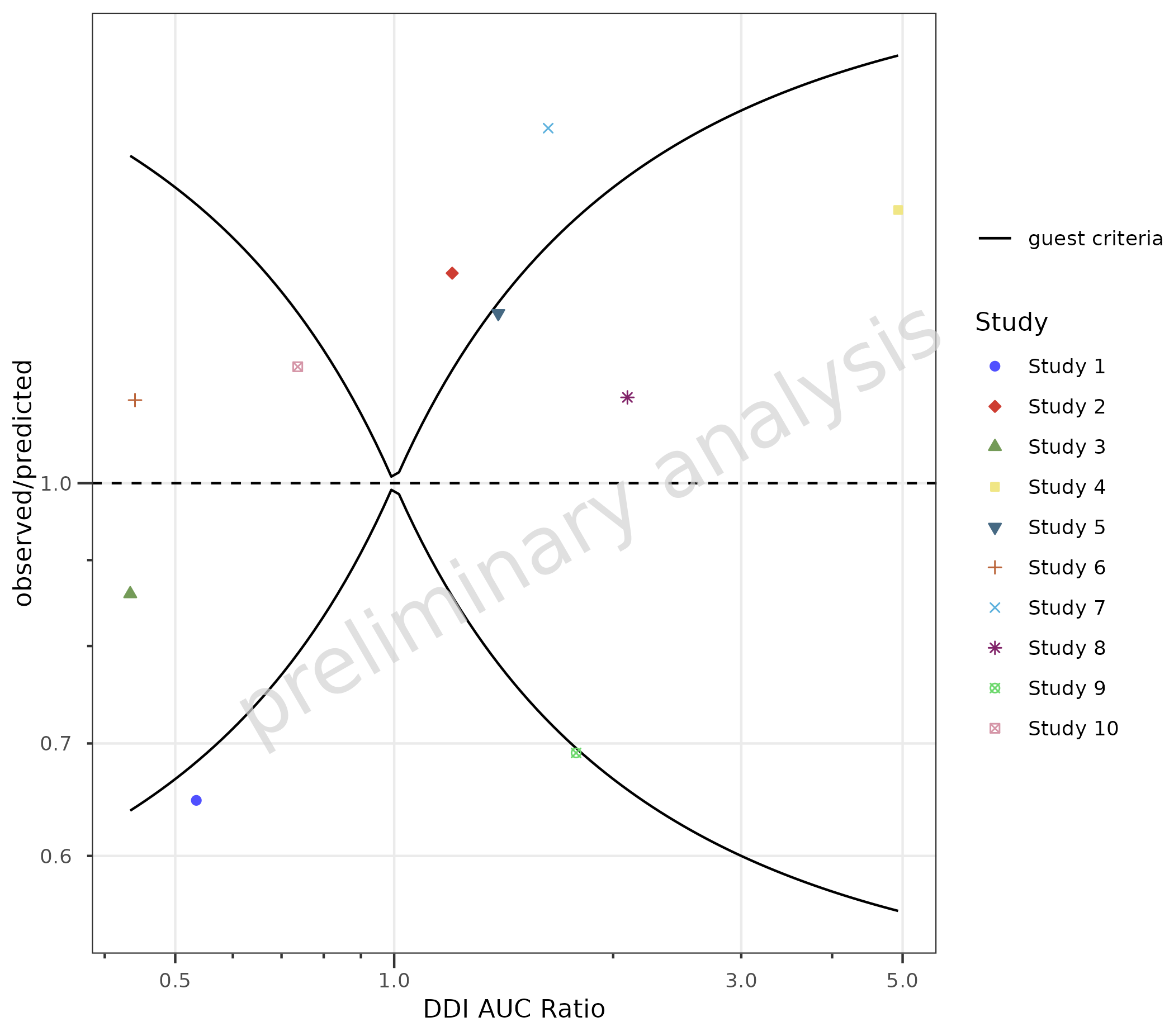
4.3 Add Guest Criteria Lines

To compare DDI ratios, set the variable addGuestLimits to TRUE and set the variable deltaGuest.

plotObject <- plotRatioVsCov(
  data = dDIdata,
  mapping = aes(
    x = Obs,
    predicted = Pred,
    observed = Obs,
    groupby = Study
  ),
  metaData = dDImetaData,
  addGuestLimits = TRUE,
  comparisonLineVector = 1
)

print(plotObject)
knitr::kable(plotObject$countsWithin)

group	Points total	guest criteria Number	guest criteria Fraction
all Groups	10	6	0.6
Study 1	1	0	0.0
Study 2	1	0	0.0
Study 3	1	1	1.0
Study 4	1	1	1.0
Study 5	1	1	1.0
Study 6	1	1	1.0
Study 7	1	0	0.0
Study 8	1	1	1.0
Study 9	1	0	0.0
Study 10	1	1	1.0

Scatter plot showing predicted versus observed DDI ratios with Guest criteria lines indicating acceptable ranges for drug-drug interaction assessment. Different studies are represented in different colors, and the plot effectively visualizes the prediction accuracy against the Guest criteria.

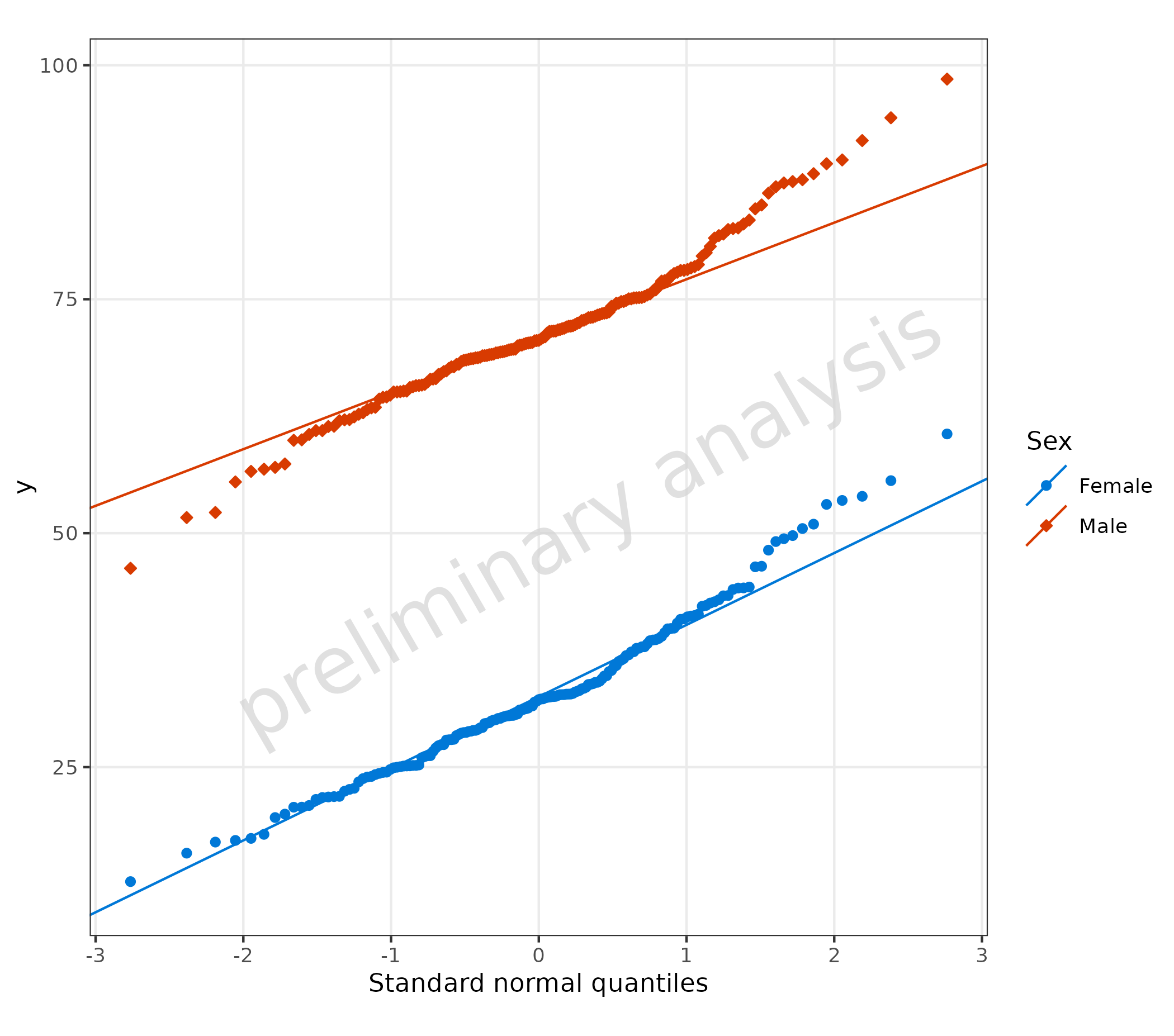
5. Quantile Plot (`plotQQ()`)

plotQQ() produces a Quantile-Quantile plot. If using the aesthetics predicted and observed, residuals will be calculated according to the variable residualScale. In the example below, the default value log is used.

plotQQ(
  data = data,
  mapping = aes(
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  )
)

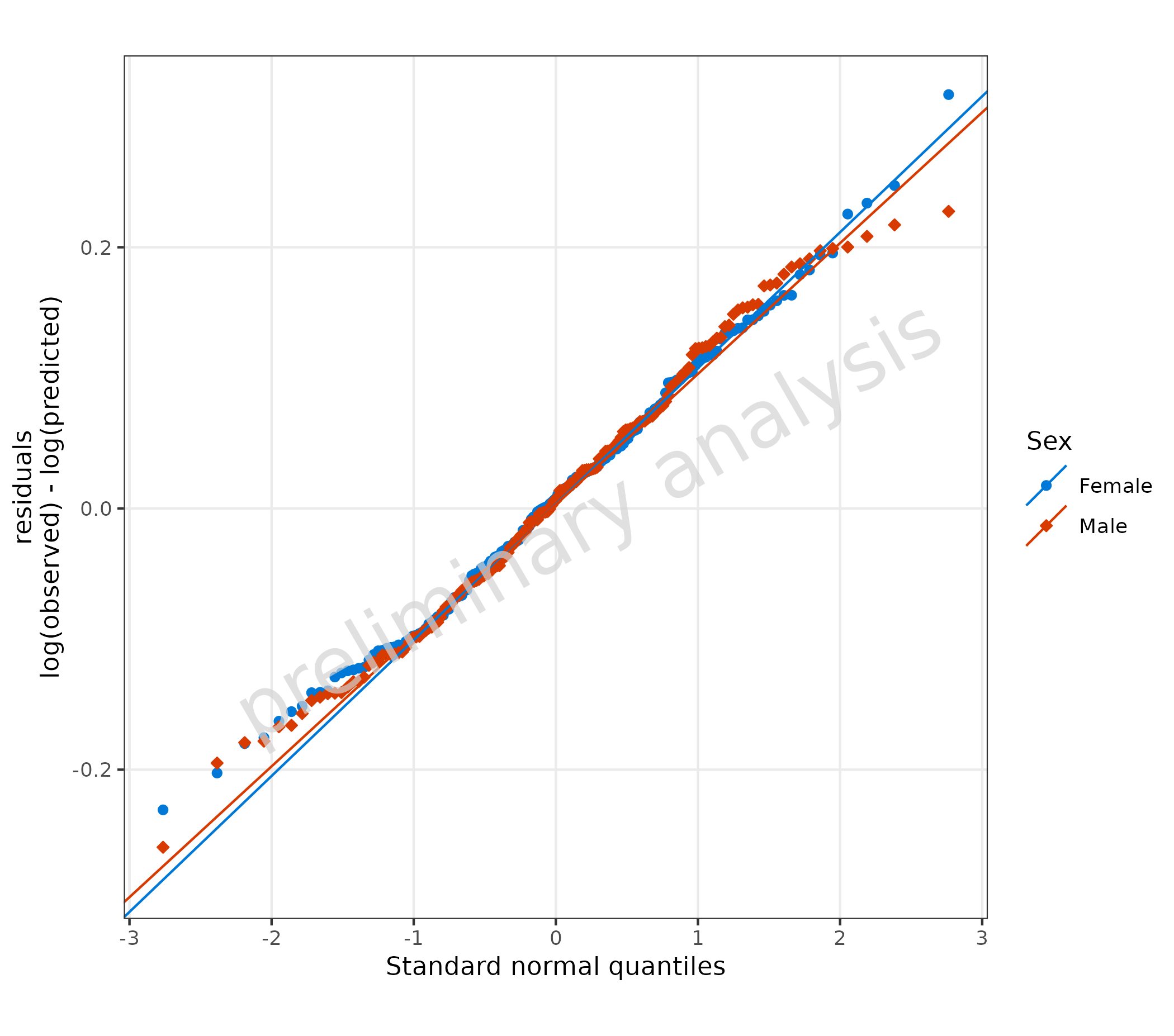
Quantile-quantile plot showing the distribution of log residuals compared to a normal distribution. Points follow the diagonal reference line if residuals are normally distributed. Deviations from the line indicate non-normal distribution patterns. Points are colored by sex groups.

The aesthetic ‘sample’ columns with already calculated residuals or formulas can be mapped directly.

plotQQ(
  data = data,
  mapping = aes(
    sample = Obs,
    predicted = Pred,
    groupby = Sex
  ),
  residualScale = "linear"
)

Quantile-quantile plot with sample data mapped directly to observed values and linear residual scale. This demonstrates mapping pre-calculated values directly using the sample aesthetic instead of automatic residual calculation. Points are colored by sex groups.

6 Usage of Aesthetics `predicted` and `observed` in Other Functions

The aesthetics observed and predicted can also be used in the functions plotHistogram() and plotBoxWhisker(). The residuals will be calculated as defined by the variable residualScale.

6.1 Residuals as Histogram

plotHistogram(
  data = data,
  metaData = metaData,
  mapping = aes(
    predicted = Pred,
    observed = Obs,
    groupby = Sex
  ),
  residualScale = "log",
  plotAsFrequency = TRUE,
  distribution = "normal"
) + geom_vline(xintercept = 0, linetype = "dashed")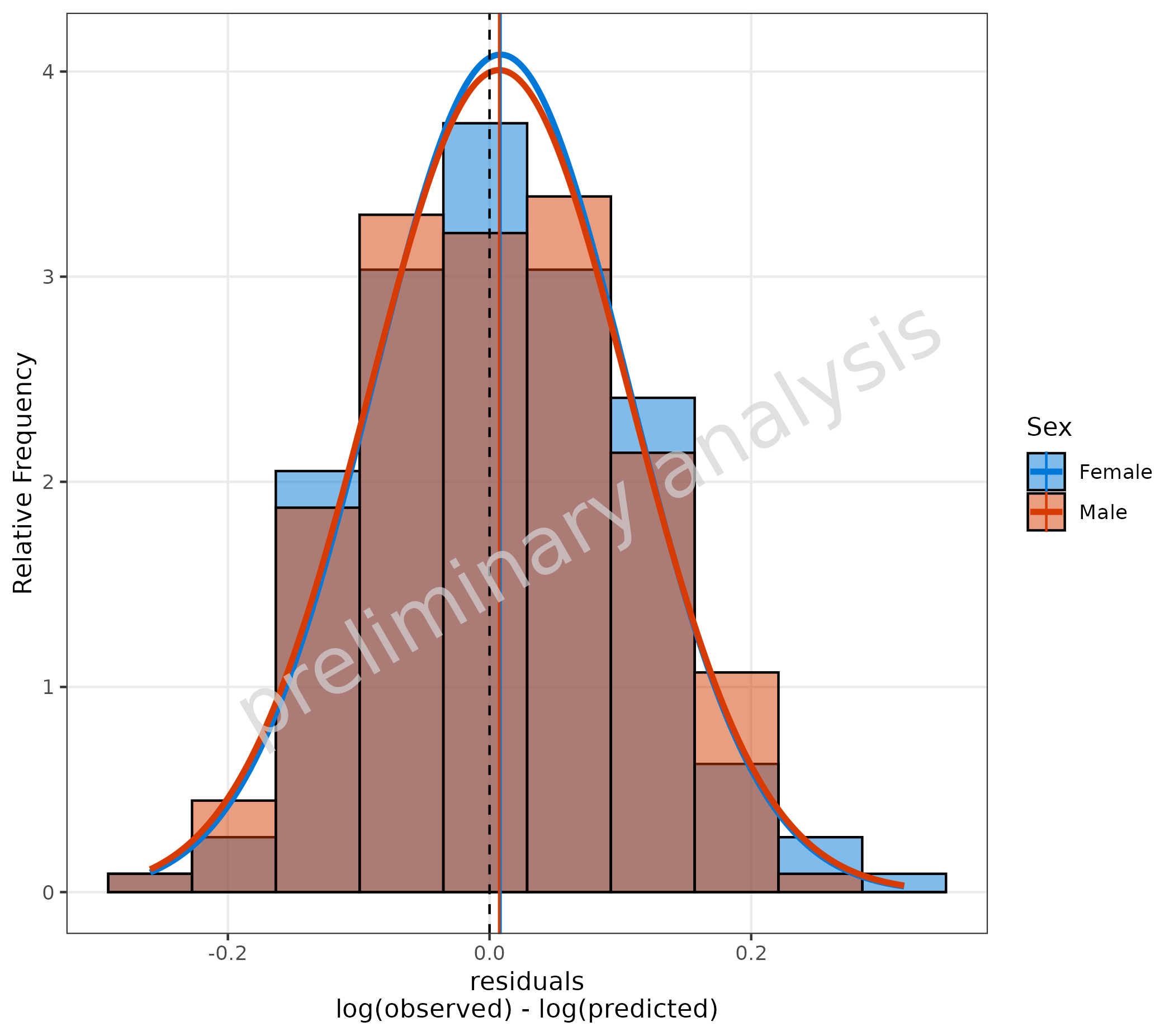

Histogram showing the distribution of log residuals with normal distribution overlay curve. The frequency-based histogram includes a dashed vertical line at zero and a fitted normal distribution curve to assess whether residuals follow a normal distribution. Histograms are stratified by sex groups.

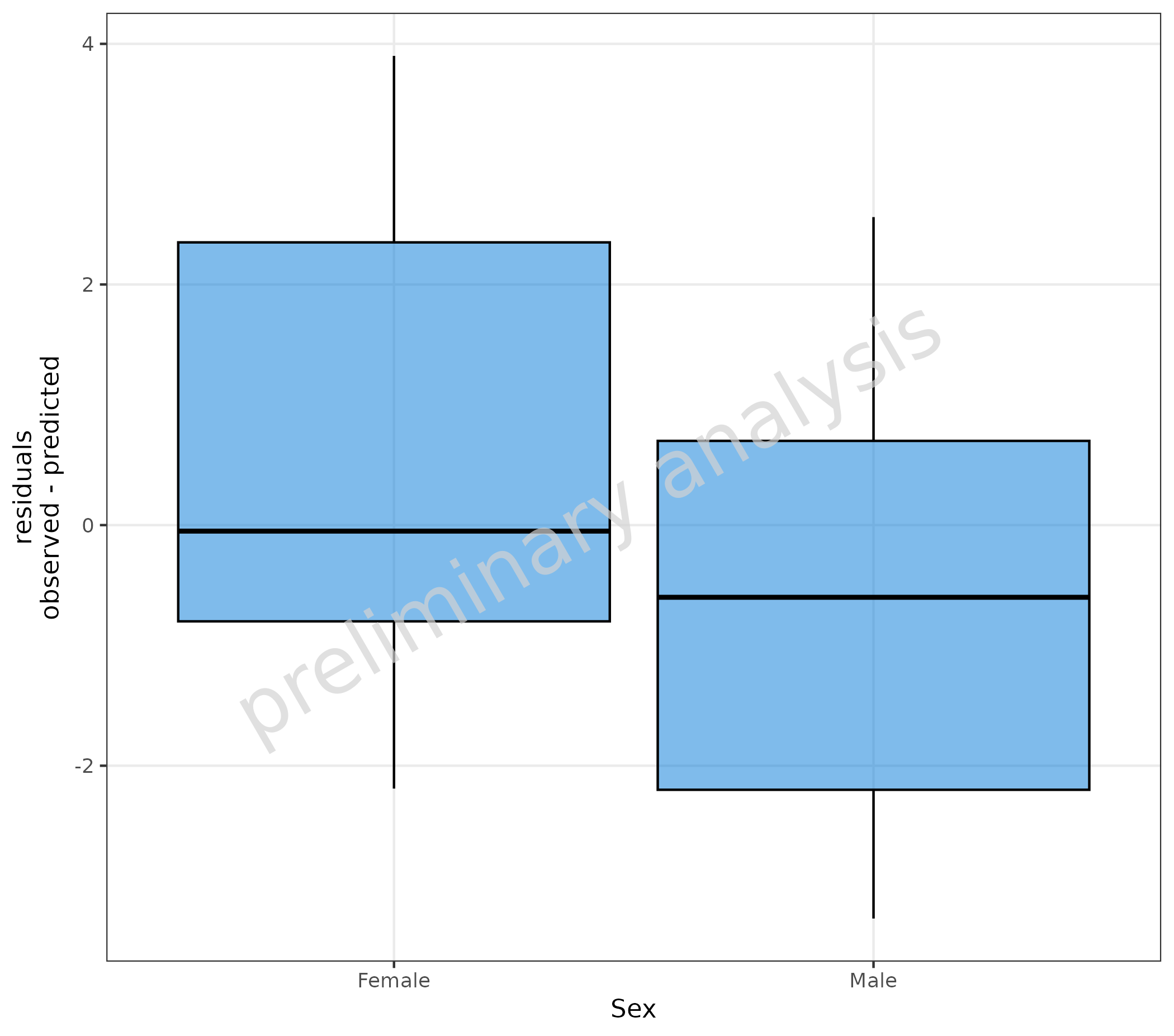
6.2 Stratify Residuals with a Box-Whisker Plot

plotBoxWhisker(
  mapping = aes(
    predicted = Pred,
    observed = Obs,
    x = Sex
  ),
  data = pkRatioData,
  metaData = metaData,
  residualScale = "linear"
)

Box plots showing the distribution of linear residuals stratified by sex. The box plots display quartiles and whiskers for residuals calculated as observed minus predicted, allowing comparison of residual distributions between male and female groups.